
- Artificial Intelligence Tutorial
- AI - Home
- AI - Overview
- AI - History & Evolution
- AI - Types
- AI - Terminology
- AI - Tools & Frameworks
- AI - Applications
- AI - Real Life Examples
- AI - Ethics & Bias
- AI - Challenges
- Branches in AI
- AI - Research Areas
- AI - Machine Learning
- AI - Natural Language Processing
- AI - Computer Vision
- AI - Robotics
- AI - Fuzzy Logic Systems
- AI - Neural Networks
- AI - Evolutionary Computation
- AI - Swarm Intelligence
- AI - Cognitive Computing
- Intelligent Systems in AI
- AI - Intelligent Systems
- AI - Components of Intelligent Systems
- AI - Types of Intelligent Systems
- Agents & Environment
- AI - Agents and Environments
- Problem Solving in AI
- AI - Popular Search Algorithms
- AI - Constraint Satisfaction
- AI - Constraint Satisfaction Problem
- AI - Formal Representation of CSPs
- AI - Types of CSPs
- AI - Methods for Solving CSPs
- AI - Real-World Examples of CSPs
- Knowledge in AI
- AI - Knowledge Based Agent
- AI - Knowledge Representation
- AI - Knowledge Representation Techniques
- AI - Propositional Logic
- AI - Rules of Inference
- AI - First-order Logic
- AI - Inference Rules in First Order Logic
- AI - Knowledge Engineering in FOL
- AI - Unification in First Order Logic (FOL)
- AI - Resolution in First Order Logic (FOL)
- AI - Forward Chaining and backward chaining
- AI - Backward Chaining vs Forward Chaining
- Expert Systems in AI
- AI - Expert Systems
- AI - Applications of Expert Systems
- AI - Advantages & Limitations of Expert Systems
- AI - Applications
- AI - Predictive Analytics
- AI - Personalized Customer Experiences
- AI - Manufacturing Industry
- AI - Healthcare Breakthroughs
- AI - Decision Making
- AI - Business
- AI - Banking
- AI - Autonomous Vehicles
- AI - Automotive Industry
- AI - Data Analytics
- AI - Marketing
Artificial Intelligence - Formal Representation of CSPs
A Constraint Satisfaction Problem (CSP) is used to find a solution that involves following a predefined conditions and rules. It is commonly used in puzzle solving, or in resource scheduling where resources allocated based on certain constraints and task planning where constraint include following a specific order.
Three primary components that make up the representation of Constraint Satisfaction Problems (CSP): variables, domains, and constraints.
Finite Set of Variables (V1,V2,...,Vn): The unknowns in the problem that require values are represented by variables. For instance, classroom seating arrangement problem, the variables are V1, V2, and V3, which stands for a student who needs to be seated.
Non-Empty Domains (D1,D2,...,Dn): Every variable has a domain of potential values. For instance, seating arrangement problem. D1={Seat1, Seat2, Seat3} V1(Student 1), D2={Seat1, Seat2, Seat3} V2 (Student 2), and so on. Each student's possible seat availability is specified by the domain.
Finite Set of Constraints (C1,C2,...,Cn): Constraints limit the values that variables can take by defining their relationships.
In a CSP, we deal with many types of restrictions on variables. Constraints help narrow down our choices to get an appropriate solution of the problem. Depending upon the number of variables affected, constraints can either be unary, binary, or of some higher order.
-
Unary Constraints: Apply to a single variable. For example: V1Seat1 (Student 1 cannot sit in Seat 1).
-
Binary Constraints: Involve two variables. For example: V1V2 (No two students can occupy the same seat).
-
Higher-Order Constraints: Involve three or more variables. For instance: V1,V2,V3 must all have distinct seat assignments.
Below is a detailed representation, along with examples and additional concepts like graph representation and arc-consistency.
Representation of Constraints in CSPs
This section covers the representation and management of CSPs. A constraint graph is a visualization tool where nodes are used to represent variables, and edges show constraints between variables. Mathematical expressions supplement this by defining the scope of restrictions (the set of variables involved) as well as valid value combinations for those variables.
All of these representations come together to form a very solid basis from which one can understand and effectively solve CSPs. Below, we explore graphical representation, mathematical formulation, and the concept of arc-consistency in detail.
Graphical Representation of CSP
A constraint graph is a graphical tool used to represent Constraint Satisfaction Problems (CSPs). It serves as a visualization of the variables' interactions with their constraints. It simplifies the structure of the problem to allow for easier analysis and solving.
Nodes: Represent the CSP's variables.
Edges: Edge indicates connection between two variables. If there is a constraint between two variables, an edge connects the nodes.
Example
In the classroom seating problem, the variables V1, V2, and V3 each represent a student's seat, and the constraint is no two students sit in the same seat.
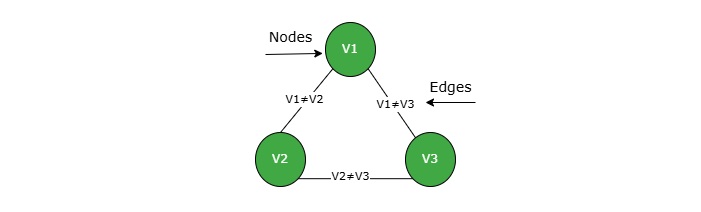
Nodes: V1: seat for student 1, V2: seat for student 2, V3: seat for student 3
Edges: V1 V2, V2 # V3, V1 V3 no students can be seated in the same seat.
The nodes represent the variables (seats for the students), edges represent constraints between the variables.
Advantages of using Graphical Representation
Following are the advantages of using graphical representation in CSP −
Constraint graphs offer a clear and understandable representation of problems.
Constraint graphs are useful for both large and small problems.
It provides a clear and intuitive way to visualize the relationships between variables and constraints.
Constraint graphs are applied in the backtracking algorithm and constraint propagation to solve CSPs in an efficient way.
Mathematical Representation of Constraints
In a mathematical representation of constraints in a CSP, each constraint is defined by a scope and a relation. The following is a mathematical representation of constraints: <Relation, Scope>. These relations represent the possible pairs of values that satisfy the specified constraint.
Scope: The set of variables that involved in the constraint.
Relation: A list of possible values that the variables can have.
Example
The following example illustrates how to represent constraints mathematically in a CSP. It illustrates the relationship between variables and their valid value combinations by using a specific situation where two variables cannot have the same value.
Constraint: V1V2
Scope: {V1,V2} (constraint-related variables).
Relation: {(Seat1, Seat2),(Seat2, Seat3),(Seat1, Seat3)} are valid combinations of values for V1 and V2.
Advantages of Mathematical Representation
Following are the advantages of mathematical representation and when to use it −
This is useful whenever you want to state and define constraints in an accurate and systematic way.
Useful for theoretical CSP analysis that requires demonstrating relationships between variables and their domains.
Arc-Consistency
Arc-consistency simplifies CSPs by reducing the domain of variables. A variable is arc-consistent if every value in its domain satisfies all constraints with the connected variables. This method is repeated recursively for all variables and constraints until no further domain reductions are possible, thus ensuring that the CSP is fully arc-consistent.
Example
This example illustrates how arc-consistency works on CSPs, by the decreasing the scope of variables gradually. It ensures that no value in one variable's domain clashes with the constraints involving by related variables, thus making the problem-solving process easier.
Constraint: V1 V2.
Domain of V1: {Seat1, Seat2, Seat3}.
Domain of V2: {Seat1, Seat2, Seat3}.
If V1=Seat1, seat1 must be removed from V2's domain to avoid violating the condition V1V2. This method continues until all variables are arc-consistent, which reduces the search space.
Advantages of Arc-Consistency
Arc-consistency enforcement improves problem-solving efficiency because it reduces incorrect possibilities as early as possible, thus reducing the overall search space and limits the need of backtracking.
-
This method helps to speed up the solution process by ensuring consistency between variables and reducing the complexity of the problem.
Note: Arc-consistency reduces the complexity of the problem but it doesn't guarantee an exact solution to all CSP problems additional algorithms are necessary for harder tasks.