Artificial Intelligence - Real-World Examples of CSPs

Quiz

Solving Traveling Sales Problem with CSP Algorithms

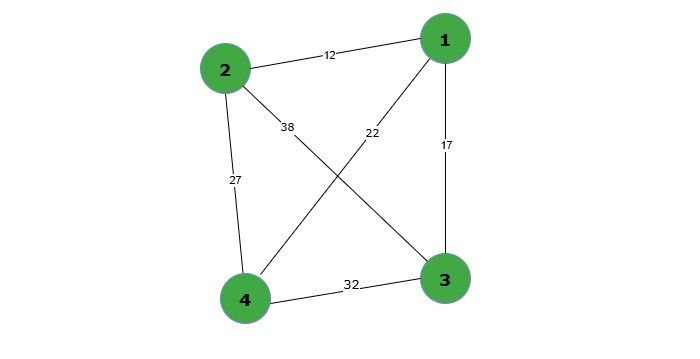
The Traveling Salesperson Problem (TSP) is to find the shortest path that travels through each city exactly once and returns to the starting city. As a Constraint Satisfaction Problem the variables, domains, and constraints of Traveling Sales Problem are listed below −

Variables: The Cities (nodes) are variables in the graph.
Domain: Any city that a salesperson visits except those cities already visited.
Constraints: Each city is visited exactly once. The traveler returns back to the start city with minimized total travel distance.

Backtracking

Backtracking is a deep-search method which is used to find a solution for complex problems. First we assign a value to the variable from its domain by following the constraint step by step and if we find the constraint is violated we go back and try a different value for previous variables.

This code utilizes backtracking to find valid paths and decide which solution is best given the following constraints.

Step 1: Define the Problem

The graph is represented as a distance matrix. Here, graph[i][j] indicates the distance between City i and City j. For example, if graph[0][1] = 12, then the distance between City 1 and City 2 is 12 units.

Here, n refers to the total number of cities, and start_node refers to the city through which the algorithm begins searching for possible routes. This structure can be seen as a basic path-finding for solving Constraint Satisfaction Problem (CSP) approaches.

# The first step is to define the graph with nodes and edges representing cities and their distances.

# Graph represented as a distance matrix
graph = [
   [0, 12, 17, 22],  # Distances from node 1
   [12, 0, 27, 38],  # Distances from node 2
   [17, 27, 0, 32],  # Distances from node 3
   [22, 38, 32, 0]   # Distances from node 4
]
n = len(graph)  # Number of nodes
start_node = 0  # Starting from node 1 (index 0)

Step 2: Define the TSP Solver Class

The TSP solver uses backtracking to explore all possible paths and find the optimal solution.

The graph and start_node are stored, and variables are initialized to track the best path and minimum cost (best_path and min_cost).

class TSP:
   def __init__(self, graph, start_node):
      self.graph = graph
      self.start_node = start_node
      self.best_path = None
      self.min_cost = float('inf')
   
   def solve(self):
      visited = [False] * len(self.graph)
      visited[self.start_node] = True
      self.backtrack([self.start_node], 0, visited)
      return self.best_path, self.min_cost
   
   def backtrack(self, path, current_cost, visited):
      # Base case: All nodes visited, return to the start
      if len(path) == len(self.graph):
         total_cost = current_cost + self.graph[path[-1]][self.start_node]
         if total_cost < self.min_cost:
            self.min_cost = total_cost
            self.best_path = path + [self.start_node]
         return
      
      # Try all possible next nodes
      for next_node in range(len(self.graph)):
         if not visited[next_node] and self.graph[path[-1]][next_node] > 0:
            visited[next_node] = True
            self.backtrack(path + [next_node], current_cost + self.graph[path[-1]][next_node], visited)
            visited[next_node] = False

Step 3: Solve the TSP Problem

We create an instance of the TSP class and call the solve method.

The solver (solve method) is then invoked to compute the optimal path and minimum cost, starting from the specified node and traversing the graph using backtracking logic.

tsp = TSP(graph, start_node)
best_path, min_cost = tsp.solve()

# Output the results
print("Optimal Path:", [node + 1 for node in best_path])  # Convert to 1-based indexing
print("Minimum Cost:", min_cost)

Complete Code

The Traveling Sales Problem (TSP) solver's complete implementation is shown below, which uses backtracking to determine the optimal path with the lowest cost.

# Graph represented as a distance matrix
graph = [
   [0, 12, 17, 22],  
   [12, 0, 27, 38],  
   [17, 27, 0, 32],  
   [22, 38, 32, 0]   
]
n = len(graph)  
start_node = 0  

class TSP:
   def __init__(self, graph, start_node):
      self.graph = graph
      self.start_node = start_node
      self.best_path = None
      self.min_cost = float('inf')
   
   def solve(self):
      visited = [False] * len(self.graph)
      visited[self.start_node] = True
      self.backtrack([self.start_node], 0, visited)
      return self.best_path, self.min_cost
   
   def backtrack(self, path, current_cost, visited):
      
      if len(path) == len(self.graph):
         total_cost = current_cost + self.graph[path[-1]][self.start_node]
         if total_cost < self.min_cost:
             self.min_cost = total_cost
             self.best_path = path + [self.start_node]
         return
      
      for next_node in range(len(self.graph)):
         if not visited[next_node] and self.graph[path[-1]][next_node] > 0:
            visited[next_node] = True
            self.backtrack(path + [next_node], current_cost + self.graph[path[-1]][next_node], visited)
            visited[next_node] = False
         
tsp = TSP(graph, start_node)
best_path, min_cost = tsp.solve()

# Output the results
print("Optimal Path:", [node + 1 for node in best_path])  
print("Minimum Cost:", min_cost)

Following is the output of the above code −

Optimal Path: [1, 2, 3, 4, 1]
Minimum Cost: 93

Print Page