Sets and Mapping in Computer Graphics

---

---

In Computer Graphics, we make full use of mathematics including set theory, trigonometry, vector algebra, linear algebra, calculus, and so on. One of the key mathematical concepts used in Graphics is sets and mappings. Sets help in structuring, organizing, and transforming data efficiently. They are fundamental in various algorithms and processes in Computer Graphics.

Read this chapter to understand the basics of sets and mappings, their application in computer graphics, and practical examples for a better understanding.

Concept of Sets in Computer Graphics

As we know form basic maths, the set is a collection of distinct objects. In computer graphics, sets are used to group data elements like points, vectors, or colors. Sets help in defining boundaries, handling data points, and performing various operations like union, intersection, and difference.

Elements and Membership in Sets

In mathematics and computer graphics, the membership of an element in a set is denoted by the symbol ∈. For instance −

$$\mathrm{a \in S}$$

This notation means that the element "a" is part of the set S. In computer graphics. Sets can be represented in a variety of objects, such as points in a 2D or 3D space.

Common sets are as follows −

• $\mathrm{R}$ − The set of all real numbers.
• $\mathrm{R^{2}}$ − The set of all ordered pairs in 2D space.
• $\mathrm{R^{3}}$ − The set of all points in 3D space.
• $\mathrm{Z}$: − The set of integers.

Cartesian Products in Sets

When we talk about sets, there is another concept called the Cartesian product. This is an operation on two sets, denoted as $\mathrm{A \times B}$, which results in a set of ordered pairs from set $\mathrm{A}$ and set $\mathrm{B}$.

For example, if set $\mathrm{A}$ contains points on a plane and set $\mathrm{B}$ contains colors, the Cartesian product can map each point to a unique color, such as −

$$\mathrm{A \times B} = \{(a1, b1), (a2, b2), (a3, b3), ...\}$$

This is particularly useful in texture mapping, where each point on a 3D model is mapped to a color or texture value.

Mappings and Functions in Computer Graphics

From two sets, if we want to find a relation, then it brings the concept of mapping. In computer graphics it has great roles for transforming sets.

A mapping or function assigns elements from one set (the domain) to elements in another set (the codomain). This can be expressed as −

$$\mathrm{f: A \rightarrow B}$$

This notation means that there is a function $\mathrm{f}$ that maps elements of set $\mathrm{A}$ to elements of set $\mathrm{B}$. Let us understand this thing visually.

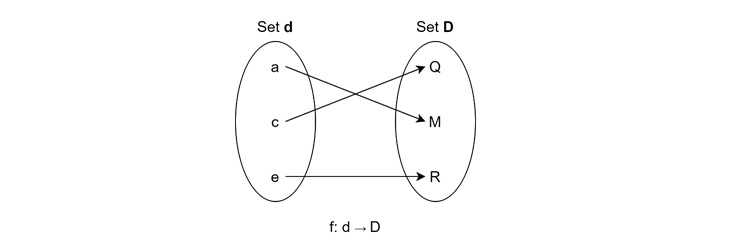
Here $\mathrm{d}$ contains $\mathrm{\{a, c, e\}}$ and $\mathrm{D}$ contains $\mathrm{\{Q, M, R\}}$. For the function $\mathrm{f: d \rightarrow D}$, the relation is being made as given in the diagram.

Domain and Range

The term domain is very common in set theory and relation. The domain of a function is the set of all possible input values, and the range is the set of all possible output values.

For instance, in a mapping where 3D coordinates (x, y, z) are transformed into 2D screen coordinates (u, v), the domain consists of the 3D points, and the range consists of the 2D screen points. The function transforms each 3D point to its 2D equivalent.

Inverse Mappings

An inverse mapping $\mathrm{f^{-1}}$ undoes the original function. $\mathrm{\text{If } f(a) = b, \text{ then } f^{-1}(b) = a}$. However, inverse mappings only exist if each element of $\mathrm{B}$ is mapped by exactly one element of $\mathrm{A}$, meaning the function must be bijective (both injective and surjective).

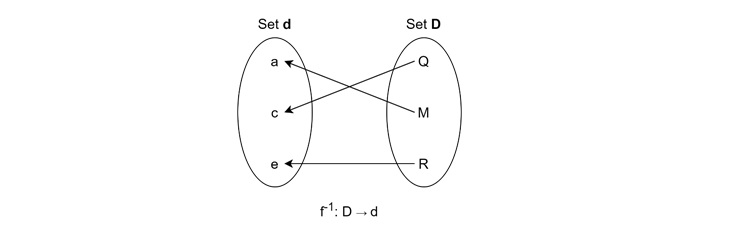
Here, it is inverse of the previously given function.

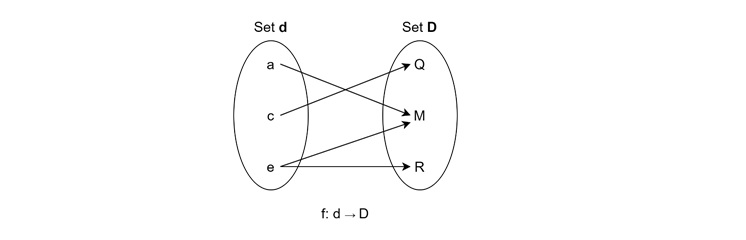
For this function, there is no inverse since it is not bijective function, and $\mathrm{M}$ is image of both $\mathrm{a}$ and $\mathrm{e}$.

Let us see example of inverse mapping. Suppose we have $\mathrm{f(x) = x^3}$, then its inverse $\mathrm{f^{-1}(x)}$ would be $\mathrm{f^{-1}(x) = \sqrt[3]{x}}$. This is because $\mathrm{f}$ assigns a unique cube to each real number, so we can "undo" the function by taking the cube root.

Types of Mappings

Functions can be categorized based on how they map elements between sets.

Injective (One-to-One) Function

A function is injective if no two elements in the domain map to the same element in the target. For example, $\mathrm{f(x) = 2x \text{ for } x \in Z}$ is injective, because each $\mathrm{x}$ produces a unique value.

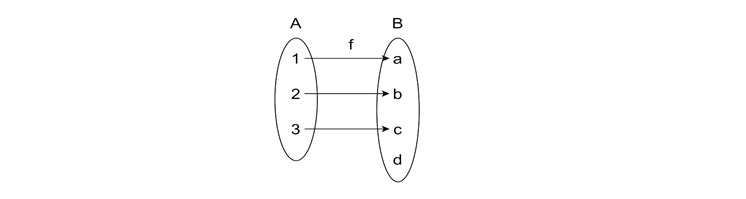
Surjective (Onto) Function

A function is surjective if every element in the target has at least one element in the domain mapping to it. For example, $\mathrm{f(x) = x^2}$ for $\mathrm{X \in R}$ is not surjective onto $\mathrm{R}$, because no real number squared gives a negative result.

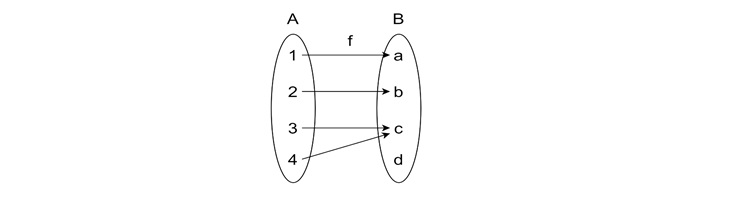
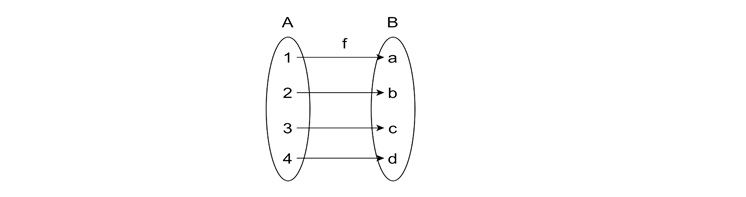
Bijective Function

A function is bijective if it is both injective and surjective. Bijective functions have inverses, which makes them particularly useful in many mathematical applications.

Intervals in Sets

An interval is a set that contains all numbers between two endpoints.

For example −

• (0,1) represents all numbers between 0 and 1, but does not include 0 or 1 (open interval).
• [0,1] includes both 0 and 1 (closed interval).

Operations on Sets

Sets can be combined or altered in various ways −

• Union (∪) − The set containing all elements from both sets. For example, {1, 2} ∪ {2, 3} = {1, 2, 3}.
• Intersection (∩) − The set containing elements common to both sets. For example, {1, 2} ∩ {2, 3} = {2}.
• Difference (-) − The set containing elements in one set but not the other. For example, {1, 2} - {2, 3} = {1}.

There are some other operations as well, but these are the most fundamental functions.

Applications of Sets in Graphics and Programming

In programming, functions (or mappings) translate inputs into outputs, much like mathematical functions. The idea of sets also plays important role. For example, in databases where records are members of a set, or in graphical coordinates where points on a screen can be viewed as elements of a 2D Cartesian set.

Also, in graphics where, we may have a function that takes a point on a 2D plane, say $\mathrm{(x, y)}$, and transforms it using a mathematical mapping. If $\mathrm{f(x, y) = (2x, 3y)}$, this stretches the point in the x direction by a factor of 2 and in the y direction by a factor of 3.

Conclusion

In this chapter, we explained the basics of sets and mappings, which are foundational concepts in both computer graphics since it is totally based on mathematics. We described what sets are, different kinds of sets, and how mappings work. We also explained inverse mappings, intervals, and operations on sets.