Trigonometry in Computer Graphics

---

---

Trigonometry plays a crucial role in computer graphics. It helps us understand and manipulate angles, distances, and positions. With trigonometry, we can utilize the idea of polar coordinates while working with viewport display, etc. In this chapter, we will see how trigonometry is used in graphics.

Basic Trigonometric Concepts

Let's understand some basic concepts of trigonometry and learn their applications with examples.

Angles in Trigonometry

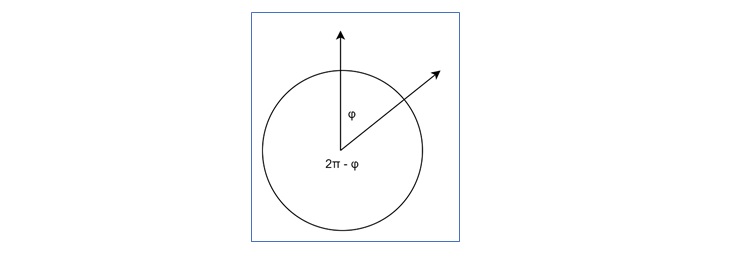
While working with trigonometry, angles are the most fundamental term. In graphics, we often work with angles. An angle is formed between two half-lines or directions. These half-lines come from a common origin. There are two possible angles between these lines. We need a convention to choose which one to use.

One common convention uses the smaller arc length as the angle. The sign of the angle is determined by the order of the half-lines. With this convention, all angles fall in the range $\mathrm{[-\pi, \pi]}$.

Angles are measured in radians or degrees. The full circle is 2 radians or 360 degrees. We can convert between these units −

• degrees $\mathrm{= \frac{180}{\pi} \times}$ radians
• radians $\mathrm{= \frac{\pi}{180} \times}$ degrees

Trigonometric Functions

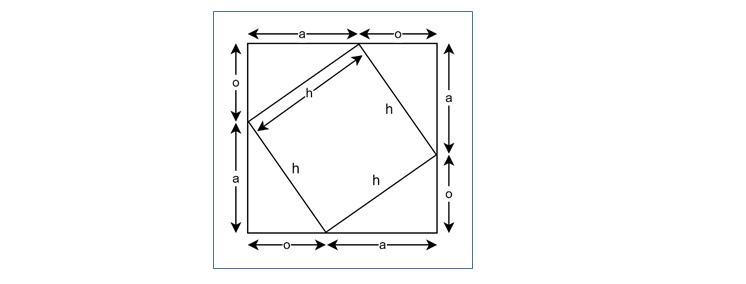
We all know the trigonometric functions that are associated with right angled triangles. In a rightangle triangle with sides a, o, and h (hypotenuse), we have the Pythagorean theorem:

$$\mathrm{a^2 + o^2 = h^2}$$

From this, we define the main trigonometric functions −

• $\mathrm{\sin \varphi = \frac{o}{h}}$
• $\mathrm{\cos \varphi = \frac{a}{h}}$
• $\mathrm{\tan \varphi = \frac{o}{a}}$

And their reciprocals −

• $\mathrm{\csc \varphi = \frac{h}{o}}$
• $\mathrm{\sec \varphi = \frac{h}{a}}$
• $\mathrm{\cot \varphi = \frac{a}{o}}$

Polar Coordinates

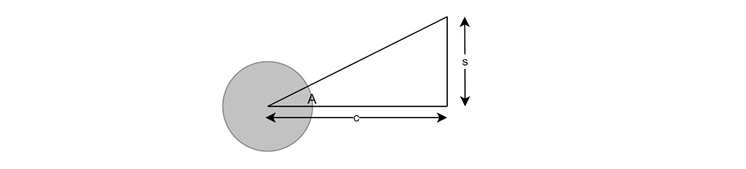
Apart from the Cartesian coordinates, there are some other coordinates one of them is the polar coordinate. In polar coordinates, we describe a point using −

• A distance from the origin (r)
• An angle relative to the positive x-axis (φ)

By convention, positive angles go counterclockwise from the x-axis.

Trigonometric Functions in Graphics

Let us see the properties for the trigonometric functions that are used in computer graphics.

Trigonometric functions are periodic. It means,

$$\mathrm{\sin(A) = \sin(A + 2\pi) \text{ for any angle } A}$$

This property is useful in animations and rotations.

Inverse Trigonometric Functions

Inverse functions are also important in graphics. Common inverse functions include −

• asin − Returns angles in $\mathrm{\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]}$
• acos − Returns angles in $\mathrm{[0, \pi]}$
• atan − Returns angles in $\mathrm{\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]}$

A special function, atan2(s,c), is very useful. It takes two values proportional to sin A and cos A. It returns the angle A. This function is often used to find the angle of a 2D point in polar coordinates.

Useful Trigonometric Identities

Let us see some key identities can simplify many graphics calculations.

Shifting Identities

These identities help when working with rotations −

• $\mathrm{\sin(-A) = -\sin(A)}$
• $\mathrm{\cos(-A) = \cos(A)}$
• $\mathrm{\sin\left(\frac{\pi}{2} - A\right) = \cos(A)}$
• $\mathrm{\cos\left(\frac{\pi}{2} - A\right) = \sin(A)}$

Pythagorean Identities

These are useful for normalizing vectors −

• $\mathrm{\sin^2 A + \cos^2 A = 1}$
• $\mathrm{\sec^2 A - \tan^2 A = 1}$

Addition and Subtraction Identities

These help when combining rotations −

• $\mathrm{\sin(A + B) = \sin A \cos B + \sin B \cos A}$
• $\mathrm{\cos(A + B) = \cos A \cos B - \sin A \sin B}$
• $\mathrm{\sin(2A) = 2 \sin A \cos A}$
• $\mathrm{\cos(2A) = \cos^2 A - \sin^2 A}$

Trigonometry in Triangle Calculations

Graphics often involve working with triangles. These formulas are helpful −

Law of Sines

For any triangle with sides a, b, c and opposite angles A, B, C −

$$\mathrm{\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}}$$

This is useful for finding unknown sides or angles.

Law of Cosines

For the same triangle −

$$\mathrm{c^2 = a^2 + b^2 - 2ab \cos C}$$

This generalizes the Pythagorean theorem to non-right triangles.

Triangle Area

The area of a triangle can be computed from its side lengths −

$$\mathrm{\text{area} = \frac{\sqrt{(a + b + c)(-a + b + c)(a - b + c)(a + b - c)}}{4}}$$

Applications of Trigonometry in Graphics

Rotations − Rotations in 2D use sin and cos −

• $\mathrm{x' = x \cos \theta - y \sin \theta}$
• $\mathrm{y' = x \sin \theta + y \cos \theta}$

Where (x,y) is the original point and (x',y') is the rotated point.

Circular Motion − Trigonometry is key for circular motion. For a circle with radius r −

• $\mathrm{x = r \cos \theta}$
• $\mathrm{y = r \sin \theta}$

As θ increases, the point (x,y) moves around the circle.

Projections − When projecting 3D objects onto 2D screens, we use trigonometry to calculate angles and distances.

Lighting − Calculating light reflections and shadows involves trigonometry. The angle between a surface normal and a light ray determines the brightness.

Conclusion

In this chapter, we explained the role of trigonometry in graphics. We covered some of the basic concepts like angles and trigonometric functions. We discussed polar coordinates and their use in graphics.

We explored the important trigonometric identities and their applications in computer graphics. We also explained how trigonometry helps in triangle calculations. Finally, we saw how these concepts apply to rotations, circular motion, projections, and lighting in graphics. These we will see later more in detail for each of these concepts.