Vectors in Computer Graphics

---

---

Vectors are frequently used in computer graphics to help us describe positions, movements, and directions in both 2D and 3D space. In this chapter, we will see the basics of vectors and their applications in graphics with examples.

Concept of Vectors

As we know from mathematics and physics, a vector is a mathematical object that has both length and direction. We can think of it as an arrow. Two vectors are the same if they have the same length and direction, even if they are in different places.

Vector Representation

We usually show vectors with letters, like 'a'. The length of a vector is written as |a|.

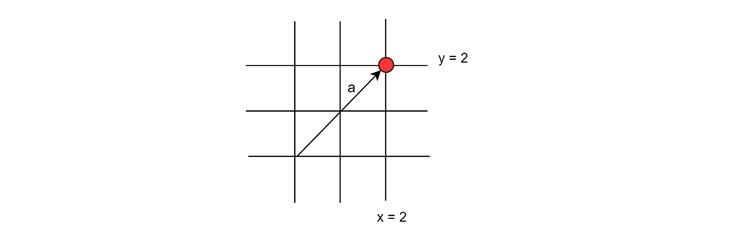
Here 'a' is a vector and it is starting from (0, 0) ending at (2, 2)

Types of Vectors

There are special types of vectors −

• Unit vector − A vector with a length of 1
• Zero vector − A vector with no length (its direction is undefined)

Uses of Vectors in Graphics

Let us talk about several use cases of vectors in computer graphics −

• Offset or Displacement − This is an interesting concept. Here vectors can show how far and in what direction to move from one point to another. For example, "go two steps east and three steps north".
• Location or Position − Another use case is based on locations. The vectors can represent a point's position relative to a starting point (origin).

Vector Operations

Let us talk about several operations associated with vectors. We call them vector algebra. We already know these things but here we will see a basic recap.

Vector Addition

The most common operation is addition for vectors. To add vectors, we use the parallelogram rule. Place the tail of one vector at the head of the other. The sum is the vector that completes the triangle.

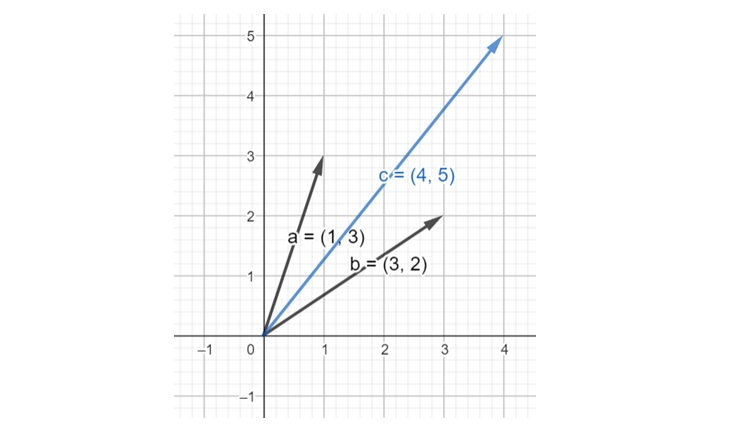
Here, the two vectors are a = (1, 3) and b = (3, 2), the addition result is c = (4, 5)

Vector Subtraction

We can subtract vectors too. It is like adding a vector in the opposite direction.

Here, the two vectors are a = (1, 3) and b = (3, 2), the addition result is c = (-2, 1)

Scaling

We can make a vector longer or shorter by multiplying it by a number. This changes its length but not its direction.

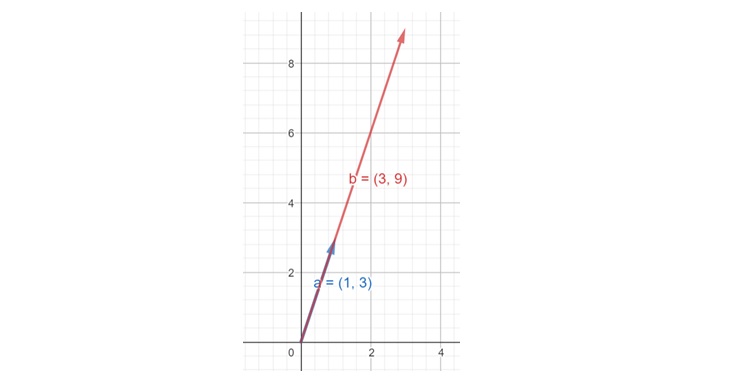
Here initial vector a = (1, 3) and after scaling by 3, b = (3, 9)

Coordinate Systems Cartesian Coordinates

We generally use a Cartesian coordinate system to describe vectors. In 2D, we use x and y coordinates. In 3D, we add a z coordinate.

Vector Representation in Coordinates

In 2D, we write a vector as (x, y) or as a column matrix −

$$\mathrm{a \:=\: \begin{bmatrix}x \\y \end{bmatrix}}$$

In 3D, we add a z component −

$$\mathrm{a \:=\: \begin{bmatrix}x \\y \\z \end{bmatrix}}$$

Let us now discuss the two types of vector products: the Dot Product and the Cross Product.

Dot Product

The dot product of two vectors gives us a single number. It is related to the vectors' lengths and the angle between them −

$$\mathrm{a \cdot b = |a| |b| \cos \phi}$$

Where φ is the angle between the vectors.

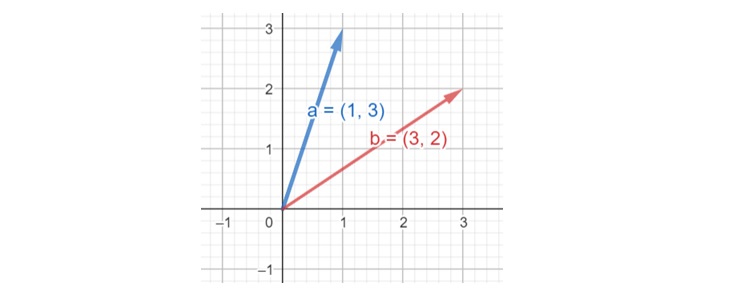
For these two vectors, the dot product returns 9.

Cross Product

The cross product is used with 3D vectors. It gives us a new vector that perpendicular to the two input vectors −

$$\mathrm{|a \times b| = |a| |b| \sin \phi}$$

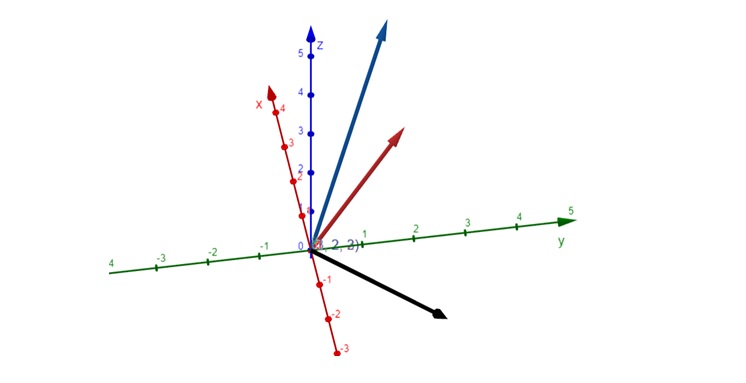
Here, a = (1, 2, 2) represented in blue, b = (3, 2, 3), represented in red, and cross product or perpendicular vector is (2, 3, -4) represented in black.

The length of this new vector is equal to the area of the parallelogram formed by the two input vectors.

Orthonormal Bases

Another interesting idea is the orthonormal basis. This is a set of vectors that are −

• At right angles to each other (orthogonal)
• Of unit length (normalized)

In 3D graphics, we often use three vectors (x, y, z) as an orthonormal basis. This forms a coordinate frame.

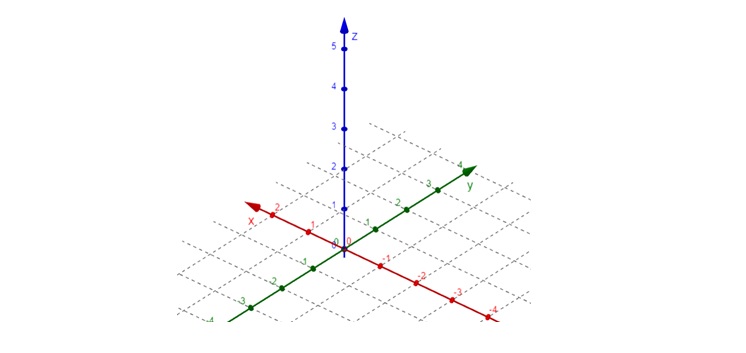
Right-Handed Coordinate System

In 3D graphics, we usually use a right-handed coordinate system. Imagine your right hand:

• Thumb points along the z-axis
• Index finger along the x-axis
• Middle finger along the y-axis

This helps us remember how the axes relate to each other.

Application of Vectors in Graphics

Vectors help us move, rotate, and scale objects in our 3D scenes. We use vectors to calculate how light interacts with surfaces in our 3D models. Vectors define where our virtual camera is and where it's looking.

Conclusion

In this chapter, we covered what vectors are and how they are represented. We also understood vector operations like addition, subtraction, and scaling. We looked at coordinate systems and how to represent vectors in them. We also discussed the two vector products: the dot product and cross product. Finally, we understood orthonormal bases and the right-handed coordinate system.