- ML - Home
- ML - Introduction
- ML - Getting Started
- ML - Basic Concepts
- ML - Ecosystem
- ML - Python Libraries
- ML - Applications
- ML - Life Cycle
- ML - Required Skills
- ML - Implementation
- ML - Challenges & Common Issues
- ML - Limitations
- ML - Reallife Examples
- ML - Data Structure
- ML - Mathematics
- ML - Artificial Intelligence
- ML - Neural Networks
- ML - Deep Learning
- ML - Getting Datasets
- ML - Categorical Data
- ML - Data Loading
- ML - Data Understanding
- ML - Data Preparation
- ML - Models
- ML - Supervised Learning
- ML - Unsupervised Learning
- ML - Semi-supervised Learning
- ML - Reinforcement Learning
- ML - Supervised vs. Unsupervised
- Machine Learning Data Visualization
- ML - Data Visualization
- ML - Histograms
- ML - Density Plots
- ML - Box and Whisker Plots
- ML - Correlation Matrix Plots
- ML - Scatter Matrix Plots
- Statistics for Machine Learning
- ML - Statistics
- ML - Mean, Median, Mode
- ML - Standard Deviation
- ML - Percentiles
- ML - Data Distribution
- ML - Skewness and Kurtosis
- ML - Bias and Variance
- ML - Hypothesis
- Regression Analysis In ML
- ML - Regression Analysis
- ML - Linear Regression
- ML - Simple Linear Regression
- ML - Multiple Linear Regression
- ML - Polynomial Regression
- Classification Algorithms In ML
- ML - Classification Algorithms
- ML - Logistic Regression
- ML - K-Nearest Neighbors (KNN)
- ML - Naïve Bayes Algorithm
- ML - Decision Tree Algorithm
- ML - Support Vector Machine
- ML - Random Forest
- ML - Confusion Matrix
- ML - Stochastic Gradient Descent
- Clustering Algorithms In ML
- ML - Clustering Algorithms
- ML - Centroid-Based Clustering
- ML - K-Means Clustering
- ML - K-Medoids Clustering
- ML - Mean-Shift Clustering
- ML - Hierarchical Clustering
- ML - Density-Based Clustering
- ML - DBSCAN Clustering
- ML - OPTICS Clustering
- ML - HDBSCAN Clustering
- ML - BIRCH Clustering
- ML - Affinity Propagation
- ML - Distribution-Based Clustering
- ML - Agglomerative Clustering
- Dimensionality Reduction In ML
- ML - Dimensionality Reduction
- ML - Feature Selection
- ML - Feature Extraction
- ML - Backward Elimination
- ML - Forward Feature Construction
- ML - High Correlation Filter
- ML - Low Variance Filter
- ML - Missing Values Ratio
- ML - Principal Component Analysis
- Reinforcement Learning
- ML - Reinforcement Learning Algorithms
- ML - Exploitation & Exploration
- ML - Q-Learning
- ML - REINFORCE Algorithm
- ML - SARSA Reinforcement Learning
- ML - Actor-critic Method
- ML - Monte Carlo Methods
- ML - Temporal Difference
- Deep Reinforcement Learning
- ML - Deep Reinforcement Learning
- ML - Deep Reinforcement Learning Algorithms
- ML - Deep Q-Networks
- ML - Deep Deterministic Policy Gradient
- ML - Trust Region Methods
- Quantum Machine Learning
- ML - Quantum Machine Learning
- ML - Quantum Machine Learning with Python
- Machine Learning Miscellaneous
- ML - Performance Metrics
- ML - Automatic Workflows
- ML - Boost Model Performance
- ML - Gradient Boosting
- ML - Bootstrap Aggregation (Bagging)
- ML - Cross Validation
- ML - AUC-ROC Curve
- ML - Grid Search
- ML - Data Scaling
- ML - Train and Test
- ML - Association Rules
- ML - Apriori Algorithm
- ML - Gaussian Discriminant Analysis
- ML - Cost Function
- ML - Bayes Theorem
- ML - Precision and Recall
- ML - Adversarial
- ML - Stacking
- ML - Epoch
- ML - Perceptron
- ML - Regularization
- ML - Overfitting
- ML - P-value
- ML - Entropy
- ML - MLOps
- ML - Data Leakage
- ML - Monetizing Machine Learning
- ML - Types of Data
- Machine Learning - Resources
- ML - Quick Guide
- ML - Cheatsheet
- ML - Interview Questions
- ML - Useful Resources
- ML - Discussion
Machine Learning - Backward Elimination
Backward Elimination is a feature selection technique used in machine learning to select the most significant features for a predictive model. In this technique, we start by considering all the features initially, and then we iteratively remove the least significant features until we get the best subset of features that gives the best performance.
Implementation in Python
To implement Backward Elimination in Python, you can follow these steps −
Import the necessary libraries: pandas, numpy, and statsmodels.api.
import pandas as pd import numpy as np import statsmodels.api as sm
Load your dataset into a Pandas DataFrame. We will be using Pima-Indians-Diabetes dataset
diabetes = pd.read_csv(r'C:\Users\Leekha\Desktop\diabetes.csv')
Define the predictor variables (X) and the target variable (y).
X = dataset.iloc[:, :-1].values y = dataset.iloc[:, -1].values
Add a column of ones to the predictor variables to represent the intercept.
X = np.append(arr = np.ones((len(X), 1)).astype(int), values = X, axis = 1)
Use the Ordinary Least Squares (OLS) method from the statsmodels library to fit the multiple linear regression model with all the predictor variables.
X_opt = X[:, [0, 1, 2, 3, 4, 5]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit()
Check the p-values of each predictor variable and remove the one with the highest p-value (i.e., the least significant).
regressor_OLS.summary()
Repeat steps 5 and 6 until all the remaining predictor variables have a p-value below the significance level (e.g., 0.05).
X_opt = X[:, [0, 1, 3, 4, 5]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() regressor_OLS.summary() X_opt = X[:, [0, 3, 4, 5]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() regressor_OLS.summary() X_opt = X[:, [0, 3, 5]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() regressor_OLS.summary() X_opt = X[:, [0, 3]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() regressor_OLS.summary()
The final subset of predictor variables with p-values below the significance level is the optimal set of features for the model.
Example
Here is the complete implementation of Backward Elimination in Python −
# Importing the necessary libraries import pandas as pd import numpy as np import statsmodels.api as sm # Load the diabetes dataset diabetes = pd.read_csv(r'C:\Users\Leekha\Desktop\diabetes.csv') # Define the predictor variables (X) and the target variable (y) X = diabetes.iloc[:, :-1].values y = diabetes.iloc[:, -1].values # Add a column of ones to the predictor variables to represent the intercept X = np.append(arr = np.ones((len(X), 1)).astype(int), values = X, axis = 1) # Fit the multiple linear regression model with all the predictor variables X_opt = X[:, [0, 1, 2, 3, 4, 5, 6, 7, 8]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() # Check the p-values of each predictor variable and remove the one # with the highest p-value (i.e., the least significant) regressor_OLS.summary() # Repeat the above step until all the remaining predictor variables # have a p-value below the significance level (e.g., 0.05) X_opt = X[:, [0, 1, 2, 3, 5, 6, 7, 8]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() regressor_OLS.summary() X_opt = X[:, [0, 1, 3, 5, 6, 7, 8]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() regressor_OLS.summary() X_opt = X[:, [0, 1, 3, 5, 7, 8]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() regressor_OLS.summary() X_opt = X[:, [0, 1, 3, 5, 7]] regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit() regressor_OLS.summary()
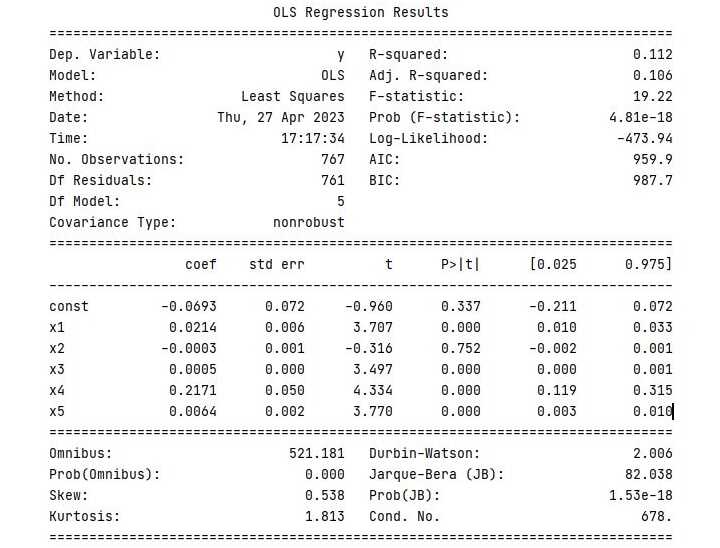
Output
When you execute this program, it will produce the following output −