
- ML - Home
- ML - Introduction
- ML - Getting Started
- ML - Basic Concepts
- ML - Ecosystem
- ML - Python Libraries
- ML - Applications
- ML - Life Cycle
- ML - Required Skills
- ML - Implementation
- ML - Challenges & Common Issues
- ML - Limitations
- ML - Reallife Examples
- ML - Data Structure
- ML - Mathematics
- ML - Artificial Intelligence
- ML - Neural Networks
- ML - Deep Learning
- ML - Getting Datasets
- ML - Categorical Data
- ML - Data Loading
- ML - Data Understanding
- ML - Data Preparation
- ML - Models
- ML - Supervised Learning
- ML - Unsupervised Learning
- ML - Semi-supervised Learning
- ML - Reinforcement Learning
- ML - Supervised vs. Unsupervised
- Machine Learning Data Visualization
- ML - Data Visualization
- ML - Histograms
- ML - Density Plots
- ML - Box and Whisker Plots
- ML - Correlation Matrix Plots
- ML - Scatter Matrix Plots
- Statistics for Machine Learning
- ML - Statistics
- ML - Mean, Median, Mode
- ML - Standard Deviation
- ML - Percentiles
- ML - Data Distribution
- ML - Skewness and Kurtosis
- ML - Bias and Variance
- ML - Hypothesis
- Regression Analysis In ML
- ML - Regression Analysis
- ML - Linear Regression
- ML - Simple Linear Regression
- ML - Multiple Linear Regression
- ML - Polynomial Regression
- Classification Algorithms In ML
- ML - Classification Algorithms
- ML - Logistic Regression
- ML - K-Nearest Neighbors (KNN)
- ML - Naïve Bayes Algorithm
- ML - Decision Tree Algorithm
- ML - Support Vector Machine
- ML - Random Forest
- ML - Confusion Matrix
- ML - Stochastic Gradient Descent
- Clustering Algorithms In ML
- ML - Clustering Algorithms
- ML - Centroid-Based Clustering
- ML - K-Means Clustering
- ML - K-Medoids Clustering
- ML - Mean-Shift Clustering
- ML - Hierarchical Clustering
- ML - Density-Based Clustering
- ML - DBSCAN Clustering
- ML - OPTICS Clustering
- ML - HDBSCAN Clustering
- ML - BIRCH Clustering
- ML - Affinity Propagation
- ML - Distribution-Based Clustering
- ML - Agglomerative Clustering
- Dimensionality Reduction In ML
- ML - Dimensionality Reduction
- ML - Feature Selection
- ML - Feature Extraction
- ML - Backward Elimination
- ML - Forward Feature Construction
- ML - High Correlation Filter
- ML - Low Variance Filter
- ML - Missing Values Ratio
- ML - Principal Component Analysis
- Reinforcement Learning
- ML - Reinforcement Learning Algorithms
- ML - Exploitation & Exploration
- ML - Q-Learning
- ML - REINFORCE Algorithm
- ML - SARSA Reinforcement Learning
- ML - Actor-critic Method
- ML - Monte Carlo Methods
- ML - Temporal Difference
- Deep Reinforcement Learning
- ML - Deep Reinforcement Learning
- ML - Deep Reinforcement Learning Algorithms
- ML - Deep Q-Networks
- ML - Deep Deterministic Policy Gradient
- ML - Trust Region Methods
- Quantum Machine Learning
- ML - Quantum Machine Learning
- ML - Quantum Machine Learning with Python
- Machine Learning Miscellaneous
- ML - Performance Metrics
- ML - Automatic Workflows
- ML - Boost Model Performance
- ML - Gradient Boosting
- ML - Bootstrap Aggregation (Bagging)
- ML - Cross Validation
- ML - AUC-ROC Curve
- ML - Grid Search
- ML - Data Scaling
- ML - Train and Test
- ML - Association Rules
- ML - Apriori Algorithm
- ML - Gaussian Discriminant Analysis
- ML - Cost Function
- ML - Bayes Theorem
- ML - Precision and Recall
- ML - Adversarial
- ML - Stacking
- ML - Epoch
- ML - Perceptron
- ML - Regularization
- ML - Overfitting
- ML - P-value
- ML - Entropy
- ML - MLOps
- ML - Data Leakage
- ML - Monetizing Machine Learning
- ML - Types of Data
- Machine Learning - Resources
- ML - Quick Guide
- ML - Cheatsheet
- ML - Interview Questions
- ML - Useful Resources
- ML - Discussion
Deep Q-Networks (DQN)
What are Deep Q-Networks?
A Deep Q-Network (DQN) is an algorithm in the field of reinforcement learning. It is a combination of deep neural networks and Q-learning, enabling agents to learn optimal policies in complex environments. While the traditional Q-learning works effectively for environments with a small and finite number of states, but it struggles with large or continuous state spaces due to the size of the Q-table. This limitation is overruled by Deep Q-Networks by replacing the Q-table with neural network that can approximate the Q-values for every state-action pair.
Key Components of Deep Q-Networks
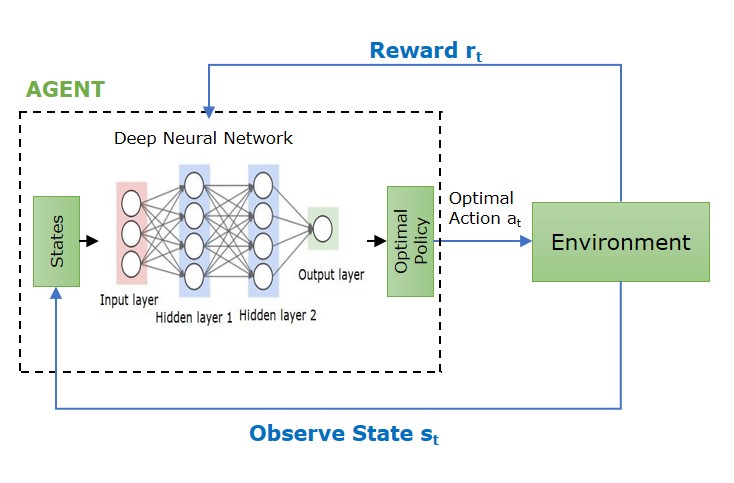
Following is a list of components that are a part of the architecture of Deep Q-Networks −
- Input Layer − This layer receives state information from the environment in the form of a vector of numerical values.
- Hidden Layers − The DQN's hidden layer consist of multiple fully connected neuron that transform the input data into more complex features that ate more suitable for predictions.
- Output Layer − Each possible action in the current state is represented by a single neuron in the DQN's output layer. The output values of these neurons represent the estimated value of each action within that state.
- Memory − DQN utilizes a memory replay to store the training events of the agent. All the information including the current state, action taken, the reward received, and the next state are stored as tuples in the memory.
- Loss Function − the DQN computes the difference between the actual Q-values form replay memory and predicted Q-values to determine loss.
- Optimization − It involves adjusting the network's weights in order to minimize the loss function. Usually, stochastic gradient descent (SGD) is employed for this purpose.
The following image depicts the components in the deep q-network architecture -
How Deep Q-Networks Work?
The working of DQN involves the following steps −
Neural Network Architecture −
The DQN uses a sequence of frames (such as images from a game) for input and generates a set of Q-values for every potential action at that particular state. the typical configuration includes convolutional layers for spatial relationships and fully connected layers for Q-values output.
Experience Replay
While training, the agent stores its interactions (state, action, reward, next state) in a replay buffer. Sampling random batches from this buffer trains the network, reducing correlation between consecutive experiences and improve training stability.
Target Network
In order to stabilize the training process, Deep Q-Networks employ a distinct target network for producing Q-value targets. the target network receives regular updates of weighs from the main network to minimize divergence risk while training.
Epsilon-Greedy Policy
The agent uses an epsilon-greedy strategy, where it selects a random action with probability ${\epsilon}$ and the action with highest Q-value with probability ${1- \epsilon}$. This balance between exploration and exploitation helps the agent learn effectively.
Training Process
The neural network is trained using gradient descent to minimize the loss between the predicted Q-values and the target Q-values. The target Q-values are calculated using the Bellman equation, which incorporates the reward received and the maximum Q-value of the nect state.
Limitations of Deep Q-Networks
Deep Q-Networks (DQNs) have several limitations that impacts it's efficiency and performance −
- DQN's suffer from instability due to the non-stationarity problem caused from frequent neural network updates.
- DQN's at times over estimate Q-values, which might have an negative impact on the learning process.
- DQN's require many samples to learn well, which can be expensive and time-consuming in terms of computation.
- DQN performance is greatly influence by the selection of hyper parameters, such as learning rate, discount factor, and exploration rate.
- DQNs are mainly intended for discrete action spaces and might face difficulties in environments with continuous action spaces.
Double Deep Q-Networks
Double DQN is an extended version of Deep Q-Network created to address an issues in the basic DQN method − Overestimation bias in Q-value updates. The overestimation bias is caused by the fact that the Q-learning update rule utilizes the same Q-network for choosing and assessing actions, resulting in inflated estimates of the Q-values. This problem can cause instability in training and hinder the learning process. The two different networks used in Double DQN to solve this issue −
- Q-Networks, responsible for choosing the action
- Target Network, assess the worth of the chosen action.
The major modification in Double DQN lies in how the target is calculated. Rather than using only Q-network for choosing and assessing the next action, Double DQN involves using the Q-network for selecting the action in the subsequent state and the target network for evaluating the Q-value of the chosen action. This separation decreases the tendency to overestimate and results in more precise value calculations. Due to this, Double DQN offers a more consistent and dependable training process, especially in scenarios such as Atari games, where the regular DQN approach may face challenges with overestimation.
Dueling Deep Q-Networks
Dueling Deep Q-Networks (Dueling DQN), improves the learning process of the traditional Deep Q-Network (DQN) by separating the estimation of state values from action advantages. In the traditional DQN, an individual Q-value is calculated for every state-action combination, representing the expected cumulative reward. However, this can be inefficient, particularly when numerous actions result in similar consequences. Dueling DQN handles this issue by breaking down the Q-value into two primary parts: the state value ${V(s)}$ and the advantage function ${A(s,a)}$. The Q-value is then given by ${Q(s,a)= V(s) + A(s,a)}$, where V(s) captures the value of being in a given state, and ${A(s,a)}$ measures how much better an action is over others in the same state.
Dueling DQN helps the agent to enhance its understanding of the environment and prevent the learning of unnecessary action-value estimates by separately estimating state values and action advantages. This results in improved performance, particularly in situations with delayed rewards, allowing the agent to gain a better understanding of the importance of various states when choosing the optimal action.