Machine Learning - Principal Component Analysis

Previous
Quiz
Next

Principal Component Analysis (PCA) is a popular unsupervised dimensionality reduction technique in machine learning used to transform high-dimensional data into a lower-dimensional representation. PCA is used to identify patterns and structure in data by discovering the underlying relationships between variables. It is commonly used in applications such as image processing, data compression, and data visualization.

PCA works by identifying the principal components (PCs) of the data, which are linear combinations of the original variables that capture the most variation in the data. The first principal component accounts for the most variance in the data, followed by the second principal component, and so on. By reducing the dimensionality of the data to only the most significant PCs, PCA can simplify the problem and improve the computational efficiency of downstream machine learning algorithms.

The steps involved in PCA are as follows −

  • Standardize the data − PCA requires that the data be standardized to have zero mean and unit variance.

  • Compute the covariance matrix − PCA computes the covariance matrix of the standardized data.

  • Compute the eigenvectors and eigenvalues of the covariance matrix − PCA then computes the eigenvectors and eigenvalues of the covariance matrix.

  • Select the principal components − PCA selects the principal components based on their corresponding eigenvalues, which indicate the amount of variation in the data explained by each component.

  • Project the data onto the new feature space − PCA projects the data onto the new feature space defined by the selected principal components.

Example

Here is an example of how you can implement PCA in Python using the scikit-learn library −

# Import the necessary libraries
import numpy as np
from sklearn.decomposition import PCA

# Load the iris dataset
from sklearn.datasets import load_iris
iris = load_iris()

# Define the predictor variables (X) and the target variable (y)
X = iris.data
y = iris.target

# Standardize the data
X_standardized = (X - np.mean(X, axis=0)) / np.std(X, axis=0)

# Create a PCA object and fit the data
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_standardized)

# Print the explained variance ratio of the selected components
print('Explained variance ratio:', pca.explained_variance_ratio_)

# Plot the transformed data
import matplotlib.pyplot as plt
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

In this example, we load the iris dataset, standardize the data, and create a PCA object with two components. We then fit the PCA object to the standardized data and transform the data onto the two principal components. We print the explained variance ratio of the selected components and plot the transformed data using the first two principal components as the x and y axes.

Output

When you execute this code, it will produce the following plot as the output −

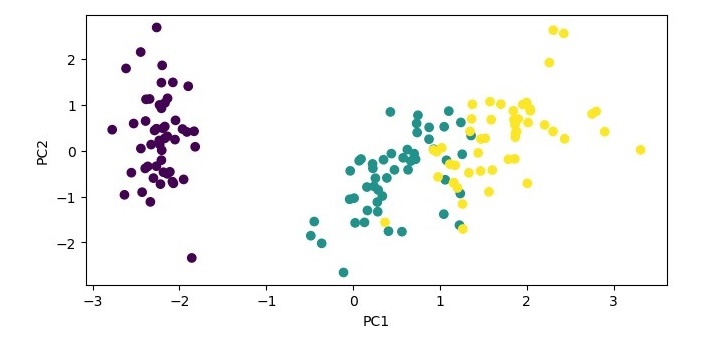
Principal Component Analysis 
Explained variance ratio: [0.72962445 0.22850762]

Advantages of PCA

Following are the advantages of using Principal Component Analysis −

  • Reduces dimensionality − PCA is particularly useful for high-dimensional datasets because it can reduce the number of features while retaining most of the original variability in the data.

  • Removes correlated features − PCA can identify and remove correlated features, which can help improve the performance of machine learning models.

  • Improves interpretability − The reduced number of features can make it easier to interpret and understand the data.

  • Reduces overfitting − By reducing the dimensionality of the data, PCA can reduce overfitting and improve the generalizability of machine learning models.

  • Speeds up computation − With fewer features, the computation required to train machine learning models is faster.

Disadvantages of PCA

Following are the disadvantages of using Principal Component Analysis −

  • Information loss − PCA reduces the dimensionality of the data by projecting it onto a lower-dimensional space, which may lead to some loss of information.

  • Can be sensitive to outliers − PCA can be sensitive to outliers, which can have a significant impact on the resulting principal components.

  • Interpretability may be reduced − Although PCA can improve interpretability by reducing the number of features, the resulting principal components may be more difficult to interpret than the original features.

  • Assumes linearity − PCA assumes that the relationships between the features are linear, which may not always be the case.

  • Requires standardization − PCA requires that the data be standardized, which may not always be possible or appropriate.

Print Page
Previous
Next
Advertisements