NumPy - Rayleigh Distribution

---

---

What is a Rayleigh Distribution?

The Rayleigh Distribution is a continuous probability distribution used to model the magnitude of a vector in a two-dimensional plane, where its components are independent and normally distributed with equal variance.

It is defined by a scale parameter (sigma). This distribution is often used in signal processing and communication theory to model scattered signals.

For example, the Rayleigh distribution can describe the distribution of wind speeds given that the wind velocity components in two orthogonal directions are independent and normally distributed.

The probability density function (PDF) of the Rayleigh distribution is defined as −

f(x; ) = (x / 2) * exp(-x2 / (22)) for x  0, 0 otherwise

Where,

• : Scale parameter (related to the standard deviation).
• x: Magnitude of the vector.
• exp: Exponential function.

Generating Rayleigh Distributions with NumPy

NumPy provides the numpy.random.rayleigh() function to generate samples from a Rayleigh distribution. You can specify the scale parameter and the size of the generated samples.

Example

In this example, we generate 10 random samples from a Rayleigh distribution with a scale parameter =1 −

import numpy as np

# Generate 10 random samples from a Rayleigh distribution with =1
samples = np.random.rayleigh(scale=1, size=10)
print("Random samples from Rayleigh distribution:", samples)

Following is the output obtained −

Random samples from Rayleigh distribution: [1.31998799 0.72631303 2.4544915  0.31195556 1.14244968 0.299947020.74889027 0.2239033  1.43290625 1.18894253]

Visualizing Rayleigh Distributions

Visualizing Rayleigh distributions helps to understand their properties better. We can use libraries such as Matplotlib to create histograms that display the distribution of generated samples.

Example

In the following example, we are first generating 1000 random samples from a rayleigh distribution with =1. We are then creating a histogram to visualize this distribution −

import numpy as np
import matplotlib.pyplot as plt

# Generate 1000 random samples from a Rayleigh distribution with =1
samples = np.random.rayleigh(scale=1, size=1000)

# Create a histogram to visualize the distribution
plt.hist(samples, bins=30, edgecolor='black', density=True)
plt.title('Rayleigh Distribution')
plt.xlabel('Magnitude')
plt.ylabel('Frequency')
plt.show()

The histogram shows the frequency of the magnitude of the vector in the Rayleigh trials. The bars represent the probability of each possible outcome, which forms the characteristic shape of a Rayleigh distribution −

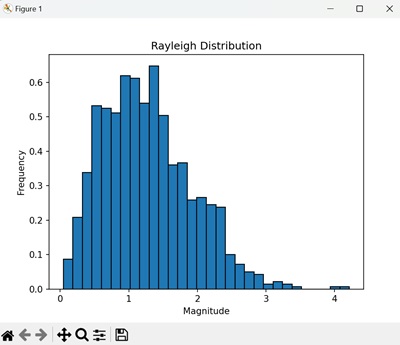
Applications of Rayleigh Distributions

Rayleigh distributions are used in various fields to model the magnitude of a vector whose components are Gaussian random variables. Here are a few practical applications −

• Signal Processing: Modeling the envelope of a signal with multiple scattered paths.
• Radar Systems: Modeling the received signal strength from targets with random scattering.
• Communication Theory: Modeling the amplitude of a signal affected by multipath fading.

Generating Cumulative Rayleigh Distributions

Sometimes, we are interested in the cumulative distribution function (CDF) of a Rayleigh distribution, which gives the probability of getting up to and including x events in the interval.

NumPy does not have a built-in function for the CDF of a Rayleigh distribution, but we can calculate it using a loop and the scipy.stats.rayleigh.cdf() function from the SciPy library.

Example

Following is an example to generate cumulative Rayleigh distribution in NumPy −

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import rayleigh

# Define the scale parameter
sigma = 1

# Generate the cumulative distribution function (CDF) values
x = np.linspace(0, 5, 100)
cdf = rayleigh.cdf(x, scale=sigma)

# Plot the CDF
plt.plot(x, cdf, marker='o', linestyle='-', color='b')
plt.title('Cumulative Rayleigh Distribution')
plt.xlabel('Magnitude')
plt.ylabel('Cumulative probability')
plt.grid(True)
plt.show()

The plot shows the cumulative probability of getting up to and including each magnitude in the Rayleigh trials. The CDF is a smooth curve that increases to 1 as the magnitude increases −

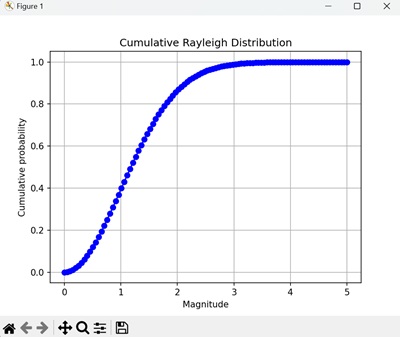
Properties of Rayleigh Distributions

Rayleigh distributions have several key properties, such as −

• Scale Parameter (): The scale parameter is related to the standard deviation of the underlying Gaussian random variables.
• Mean and Variance: The mean of a Rayleigh distribution is (/2), and the variance is (2-/2)².
• Skewness: The distribution is skewed to the right, with a long tail.

Using Rayleigh Distribution for Hypothesis Testing

Rayleigh distributions are often used in hypothesis testing, particularly in tests for the magnitude of a vector.

One common test is the Rayleigh test, which is used to determine if the observed magnitude is significantly different from the expected magnitude. Here is an example using the scipy.stats.rayleigh() function:

Example

In this example, we perform a Rayleigh test to determine if the observed magnitude (1.5) is significantly different from the expected scale (=1). The p-value indicates the probability of obtaining a result at least as extreme as the observed result, assuming the null hypothesis is true −

from scipy.stats import rayleigh

# Observed magnitude
observed_magnitude = 1.5

# Expected scale parameter ()
expected_scale = 1

# Perform the Rayleigh test
p_value = rayleigh.sf(observed_magnitude, scale=expected_scale)
print("P-value from Rayleigh test:", p_value)

The output obtained is as shown below −

P-value from Rayleigh test: 0.32465246735834974

Seeding for Reproducibility

To ensure reproducibility, you can set a specific seed before generating Rayleigh distributions. This ensures that the same sequence of random numbers is generated each time you run the code.

Example

By setting the seed, you ensure that the random generation produces the same result every time the code is executed as shown in the example below −

import numpy as np

# Set the seed for reproducibility
np.random.seed(42)

# Generate 10 random samples from a Rayleigh distribution with =1
samples = np.random.rayleigh(scale=1, size=10)
print("Random samples with seed 42:", samples)

The result produced is as follows −

Random samples with seed 42: [0.96878077 2.45361832 1.62280356 1.35125316 0.58245149 0.58240242
 0.34594441 2.00560757 1.35578918 1.56923552]