NumPy - Uniform Distribution

---

---

What is a Uniform Distribution?

A uniform distribution is a type of probability distribution where all outcomes are equally likely. This means that the probability of any given outcome is constant across the range of possible outcomes.

Uniform distributions can be continuous or discrete. In a continuous uniform distribution, the outcomes can take any value within a specified range. In contrast, a discrete uniform distribution has a finite set of possible outcomes.

Uniform Distributions with NumPy

NumPy provides the numpy.random.uniform() function to generate samples from a continuous uniform distribution. This function allows you to specify the range and size of the generated samples.

Example

In this example, we generate 10 random samples from a uniform distribution between 0 and 1 −

import numpy as np

# Generate 10 random samples from a uniform distribution between 0 and 1
samples = np.random.uniform(0, 1, 10)
print("Random samples from uniform distribution:", samples)

Following is the output obtained −

Random samples from uniform distribution: [0.70748409 0.45654756 0.73426382 0.15580835 0.70294526 0.12503631
 0.40303738  0.9862709  0.4923119  0.44059809]

Visualizing Uniform Distributions

Visualizing uniform distributions helps to understand their properties better. We can use libraries such as Matplotlib to create histograms that display the distribution of generated samples.

Example

In the following example, we are generating 1000 random samples from a uniform distribution between 0 and 1 and then create a histogram to visualize this distribution −

import numpy as np
import matplotlib.pyplot as plt

# Generate 1000 random samples from a uniform distribution between 0 and 1
samples = np.random.uniform(0, 1, 1000)

# Create a histogram to visualize the distribution
plt.hist(samples, bins=30, edgecolor='black')
plt.title('Uniform Distribution')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

The histogram shows that the samples are uniformly distributed between 0 and 1, with an approximately equal frequency for each bin −

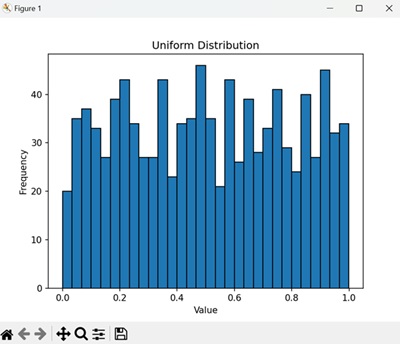
Applications of Uniform Distributions

Uniform distributions are used in various fields, including computer simulations, Monte Carlo methods, and random sampling. Here are a few practical applications −

• Simulation: Uniform distributions are used to simulate random events in models where each outcome is equally likely.
• Random Sampling: Uniform distributions are used to generate random samples from a population for statistical analysis.
• Monte Carlo Methods: Uniform distributions are used in Monte Carlo simulations to generate random numbers for estimating complex integrals and solving problems in physics and finance.

Generating Discrete Uniform Distributions

NumPy also allows generating samples from a discrete uniform distribution using the numpy.random.randint() function. This function generates random integers within a specified range.

Example

In this example, we generate 10 random integers between 1 and 10, inclusive −

import numpy as np

# Generate 10 random integers between 1 and 10
samples = np.random.randint(1, 11, 10)
print("Random samples from discrete uniform distribution:", samples)

Following is the output obtained −

Random samples from discrete uniform distribution: [ 7  3  9 10  9  4  8  4  1  7]

Properties of Uniform Distributions

Uniform distributions have several key properties, they are as follows −

• Constant Probability Density: In a continuous uniform distribution, the probability density function (PDF) is constant across the specified range.
• Equal Likelihood: All outcomes within the range are equally likely.
• Mean and Variance: For a continuous uniform distribution between a and b, the mean is (a + b) / 2 and the variance is ((b - a)²) / 12.

Calculating Mean and Variance

You can calculate the mean and variance of a uniform distribution using simple formulas. Let us see how to calculate the mean and variance for a uniform distribution between a and b.

Example

In this example, the mean and variance of the uniform distribution between 0 and 1 are calculated −

import numpy as np

# Define the range of the uniform distribution
a = 0
b = 1

# Calculate the mean and variance
mean = (a + b) / 2
variance = ((b - a) ** 2) / 12

print("Mean:", mean)
print("Variance:", variance)

Following is the output obtained −

Mean: 0.5
Variance: 0.08333333333333333

Uniform Distribution in Multidimensional Arrays

NumPy can generate uniform distributions for multidimensional arrays as well. Here is an example:

Example

In this example, a 3x3 array of random samples from a uniform distribution between 0 and 1 is generated −

import numpy as np

# Generate a 3x3 array of random samples from a uniform distribution between 0 and 1
samples = np.random.uniform(0, 1, (3, 3))
print("3x3 array of random samples from uniform distribution:", samples)

The output obtained is as shown below −

3x3 array of random samples from uniform distribution: 
[[0.18528116 0.65725829 0.06597822]
 [0.73183704 0.05931206 0.65555952]
 [0.92479579 0.89807463 0.02624335]]

Seeding for Reproducibility

To ensure reproducibility, you can set a specific seed before generating uniform distributions. This ensures that the same sequence of random numbers is generated each time you run the code.

Example

By setting the seed, you ensure that the random generation produces the same result every time the code is executed as shown in the following example −

import numpy as np

# Set the seed for reproducibility
np.random.seed(42)

# Generate 10 random samples from a uniform distribution between 0 and 1
samples = np.random.uniform(0, 1, 10)
print("Random samples with seed 42:", samples)

Following is the output obtained −

Random samples with seed 42: [0.37454012 0.95071431 0.73199394 0.59865848 0.15601864 0.15599452
 0.05808361 0.86617615 0.60111501 0.70807258]