Scipy Differential Equations

SciPy's Differential Equations module provides tools for solving ordinary differential equations (ODEs) and partial differential equations (PDEs). This module includes various functions such as scipy.integrate.odeint() and scipy.integrate.solve_ivp() which allow users to integrate ODEs using methods such as Runge-Kutta and BDF (Backward Differentiation Formulas).

These functions enable the specification of initial conditions and the handling of time-dependent problems. SciPy also supports the integration of systems of equations and provides options for adaptive step size control by making it a powerful resource for scientists and engineers modeling dynamic systems and analyzing their behaviors over time.

Key Features of Scipy Differential Equations

SciPy offers several key features for solving differential equations by making it a powerful tool for scientific and engineering applications. Below are some of the main features, let's see them one by one −

• ODE Solvers: SciPy provides a range of ordinary differential equation (ODE) solvers through the scipy.integrate.() and scipy.integrate.solve_ivp() functions. These solvers support various methods such as Runge-Kutta and can handle stiff and non-stiff problems.
• Event Handling: The solve_ivp() function includes options to detect events such as reaching a specific threshold by allowing users to stop integration when certain conditions are met.
• Integration of Initial Value Problems: The solvers can handle initial value problems for systems of ODEs by making it easy to integrate complex dynamical systems.
• Support for Time-dependent Parameters: SciPy allows the incorporation of time-dependent parameters in the equations by enabling dynamic modeling of systems where parameters change over time.
• Boundary Value Problems: The scipy.integrate.solve_bvp() function can solve boundary value problems by providing a framework for problems with conditions specified at more than one point.
• Numerical Integration: In addition to solving differential equations, SciPy includes functions for numerical integration by enabling users to compute solutions to integrals related to differential equations.
• Rich Documentation and Examples: SciPys documentation includes extensive examples and explanations which makes it easier for users to understand how to apply its functions effectively.
• Interoperability with NumPy: SciPy is built on NumPy by ensuring seamless integration with arrays and numerical operations which is essential for efficient computation in differential equations.

These features make SciPy a comprehensive toolkit for tackling various differential equation problems in scientific computing.

Applications of Scipy Differential Equations

SciPy's capabilities for solving differential equations have a wide range of applications across various fields. Here are some notable applications −

• Physics: Modeling physical systems such as harmonic oscillators, pendulums and wave equations. Differential equations describe the dynamics of particles and waves by enabling predictions about their behavior over time.
• Engineering: Analyzing systems in control theory, structural dynamics and fluid dynamics. Engineers use differential equations to model and control systems, optimize designs and ensure stability.
• Biology: This is used to simulate population dynamics, disease spread and biochemical reactions. Differential equations can model the growth of populations, the spread of infectious diseases or the rates of reaction in biological systems.
• Finance: The Differential Eqautions are used in option pricing and risk assessment often involve stochastic differential equations. These equations help model the behavior of financial instruments and assess risk in uncertain environments.
• Chemistry: This is used in modeling reaction kinetics and thermodynamics. Differential equations can describe the rate of chemical reactions and the changes in concentration of reactants and products over time.
• Environmental Science: Simulating environmental processes such as pollutant dispersion, resource management and climate modeling. Differential equations are used to predict how substances spread in ecosystems or how resources are utilized.
• Robotics and Control Systems: Used in designing and analyzing robotic systems and control strategies. Differential equations describe the dynamics of robotic movements and are essential in creating feedback control systems.
• Neuroscience: Differential equations are used to simulate the electrical activity of neurons and the interactions between different brain regions.
• Machine Learning: The differential equations can be used in some algorithms especially in reinforcement learning, rely on differential equations to model continuous state transitions or dynamics of systems being learned.
• Astrophysics: These are used in simulating celestial mechanics and stellar dynamics. Differential equations help model the motion of planets, stars and galaxies as well as the evolution of stellar objects.

These applications demonstrate the versatility of differential equations in modeling and solving real-world problems across diverse domains.

Example

Heres an example of how to solve a simple first-order ODE using the solve_ivp() function in scipy −

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# Define the ODE as a function
def ode_function(t, y):
    return -2 * y

# Initial conditions
y0 = [1]  # Initial value of y
t_span = (0, 5)  # Time interval for the solution
t_eval = np.linspace(t_span[0], t_span[1], 100)  # Points at which to store the solution

# Solve the ODE
solution = solve_ivp(ode_function, t_span, y0, t_eval=t_eval)

# Plot the results
plt.plot(solution.t, solution.y[0], label='y(t) = e^{-2t}')
plt.title('Solution of ODE')
plt.xlabel('Time t')
plt.ylabel('Function y')
plt.axhline(0, color='gray', lw=0.5, ls='--')
plt.axvline(0, color='gray', lw=0.5, ls='--')
plt.legend()
plt.grid()
plt.show()

Following is the output of the calculating the simple first order ODE using solve_ivp() function in scipy −

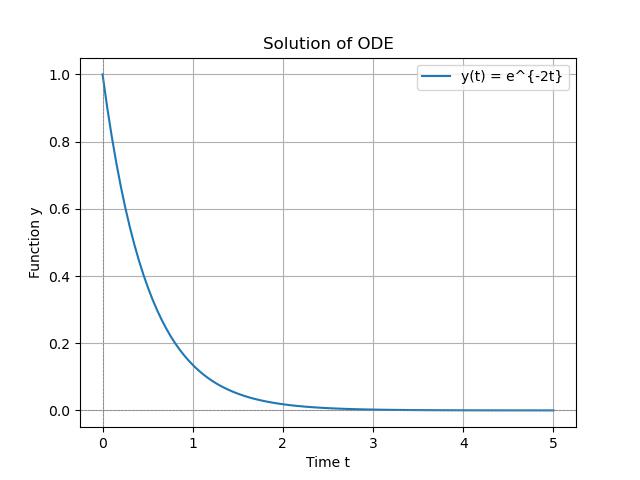
We can say sciPys capabilities for solving differential equations make it a powerful tool for scientists and engineers by enabling them to model and analyze dynamic systems effectively. Whether working with simple first-order ODEs or more complex systems SciPy provides the necessary functions to find numerical solutions and visualize results.