SciPy - Filtering and Edge Detection

---

---

What is Filtering in SciPy?

Filtering in image processing is a fundamental technique used for a variety of tasks such as noise reduction, image enhancement and feature extraction. Image filters work by modifying or processing an image's pixel values based on its neighbors or applying mathematical transformations.

In SciPy filters can be applied to images to perform operations like smoothing, sharpening and edge detection. In this chapter let's see about the key concepts, types of filters and how to implement filters using SciPy.

What is Edge Detection?

Edge detection is a crucial technique in image processing used to identify points in an image where there is a sharp contrast in pixel intensity which is often corresponding to boundaries or transitions between different regions of the image. In the view of SciPy image processing the edge detection is typically achieved by using filters that highlight areas of rapid intensity change usually via the computation of gradients or second-order derivatives.

In SciPy, edge detection can be performed using several techniques such as Sobel, Prewitt, Scharr, Roberts and Laplacian filters. These filters are applied to an image to highlight areas with significant intensity gradients which typically correspond to edges.

Before getting deep into the Filtering and Edge Detection techniques we need to understand some basics concepts for filtering as follows −

Kernel

A kernel is also known as a mask, filter or convolution matrix which is a small, matrix-shaped set of numerical weights used in image filtering. It is applied to an image by performing a mathematical operation i.e., typically convolution between the kernel and small sections of the image. This operation produces a new value for each pixel by depending on the kernel's purpose.

For a kernel K and an image I the operation at a pixel (x,y) can be expressed as follows −

Where −

• I'(x,y): Output pixel value at position (x,y).
• K(i,j): Kernel weight at offset (i,j).
• n,m: Half the width and height of the kernel e.g., for a 33 kernel n=m=1.

Role of Kernels in Filtering

Kernels are designed to perform specific operations such as mentioned below −

• Blurring: Reducing noise and smoothing images.
• Edge Detection: Highlighting boundaries and transitions.
• Enhancing Details: Sharpening fine image features.

Key Properties of Kernels

Here are the key properties of Kernels in SciPy Image Processing −

• Symmetry: Some kernels such as Gaussian are symmetric which ensure equal effects in all direction
• Normalization: Kernels like the mean filter often normalize values i.e., divide by the sum of weights to maintain intensity balance.
• Edge Effects: Handling edges of the image means where the kernel extends beyond the image boundary requires padding techniques such as zero-padding or reflection.

Types of Kernels

Following are different types of kernel which determines the effect it has on the image.

• Smoothing Kernels: These kernels reduce noise and smooth an image by averaging the intensity of neighboring pixels.
• Sharpening Kernels: It enhance the fine details and edges in an image.
• Edge Detection Kernels: These kernels are designed to find edges in an image by identifying areas with high intensity gradients.
• Embossing Kernels: These kernels hHighlights edges and gives a 3D effect to the image.
• Gradient Kernels: These type of kernels are used to calculate intensity gradients in specific directions.
• Specialized Kernels: The specialized kernels are used to focus on circular regions or to simulate motion blur along a specific direction.
• custom Kernels: Kernels can be designed for specific purposes by customizing weights.

Convolution

In image processing convolution is a mathematical operation used to apply a filter or kernel to an image. It involves sliding the kernel over the image by performing element-wise multiplication between the kernel and the image pixels under the kernel and then summing the results to get a new pixel value.

In SciPy convolution can be done using the scipy.ndimage.convolve() or scipy.signal.convolve2d() functions. These functions allow us to apply a kernel to an image, time series or multi-dimensional data.

The convolution operation between an image I and a kernel K is define d as follows −

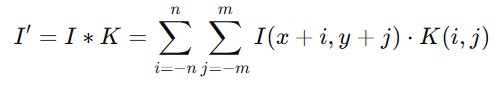
Where −

• I is the input image.
• K is the kernel or filter.
• I' is the output image or the result of convolution.
• The kernel slides over the image and the sum of element-wise products at each position gives the resulting pixel value.

Key properties of Convolution

Following are the properties which make convolution a versatile and powerful operation in image and signal processing −

• Commutativity: The order of convolution does not matter which is given as I*K = K*I.
• Associativity: The grouping of convolutions does not matter which can be refered as I*(K*L) = (I*K)*L.
• Distributivity: Convolution distributes over addition which can represented as I*(K+L) = (I*K)+(I*L).
• Identity Element: The identity kernel for example a kernel with a 1 in the center and 0s elsewhere, leaves the image unchanged when convolved.
• Shift Invariance: Convolution is unaffected by shifting the image. Shifting the image before or after convolution gives the same result.
• Linearity: Convolution is linear so we can scale images or kernels and the result will scale accordingly.
• Separable: If a 2D kernel can be separated into two 1D kernels then the convolution can be done more efficiently by applying the 1D kernels in sequence.

Types of Filters

Filters are crucial tools in image processing for enhancing, transforming or extracting features from images. There are different types of filters designed for a specific effect which depends on the desired outcome for the image processing task. Following are the types of filters −

• Low Pass Filters (Smoothing Filters)
• High Pass Filters
• Morphological Filters