SciPy - Mathematical Constants

---

---

SciPy provides a set of mathematical constants that are useful across various computational tasks. These constants are pre-defined values that are fundamental in mathematical computations and scientific research.

Below are the key mathematical constants available in SciPy and their theoretical definitions. Let's see them one by one in detail −

Euler's Number (e)

Euler's number is approximately equal to 2.71828 which is the base of the natural logarithm. It is a fundamental constant in mathematics, especially in calculus and complex analysis. It arises naturally in the study of exponential growth, compound interest and in the solutions to differential equations.

Syntax

Following is the syntax of calculating the Euler's Number with the help of SciPy −

scipy.constants.e

Example

Here's an example of how we can use Euler's Number in SciPy for computing continuous growth or decay.

import numpy as np
from scipy.constants import e

# Parameters
P0 = 1000  # Initial population
r = 0.05   # Growth rate (5% per unit time)
t = 10     # Time (10 units)

# Calculate the population at time t
P_t = P0 * np.exp(r * t)

print(f"Population after {t} units of time: {P_t}")

Following is the output of the above program −

Population after 10 units of time: 1648.7212707001281

Pi ()

Pi is the ratio of the circumference of a circle to its diameter. It is a transcendental number with an approximate value of 3.14159. This is crucial in geometry, trigonometry and various areas of science and engineering.

Syntax

Below is the syntax of calculating the Pi with the help of SciPy −

scipy.constants.pi

Example

Following is an example of how we can calculate the pi in SciPy −

import numpy as np
from scipy.constants import pi
print("Pi:",pi)

Following is the output of the above program −

Pi: 3.141592653589793

The Golden Ratio ()

The Golden ratio is denoted as (phi) and is approximately given as 1.61803 which is a special number that appears in various contexts in art, architecture and nature. It is defined algebraically as −

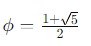
It is associated with aesthetically pleasing proportions and is seen in the Fibonacci sequence.

Syntax

Below is the syntax of calculating the Golden Ratio () with the help of SciPy −

scipy.constants.golden

Example

In SciPy the Golden Ratio is provided in the scipy.constants.golden method. Heres how we can access and use it −

from scipy.constants import golden
print(f"The Golden Ratio () is: {golden}")

Following is the output of the above program −

The Golden Ratio () is: 1.618033988749895

Avogadro Constant

Avogadro constant is represented as Avogadro or N_A. It provides the number of entities such as atoms or molecules in one mole of a substance.

The Avogadro constant is a fundamental quantity in chemistry and physics. The value of Avogadro constant is given as 6.02214076e+23 (mol).

Syntax

Here is the syntax of calculating the Avogadro constant with the help of SciPy −

scipy.constants.Avogadro

Example

Here is the example which shows how to calculate the Avogadro constant using the method scipy.constants.Avogadro −

from scipy.constants import Avogadro
# Print Avogadro's Number
print(f"Avogadro's Number (N_A) is: {Avogadro}")

Following is the output of the above program −

Avogadro's Number (N_A) is: 6.02214076e+23

Boltzmann Constant (k_B)

Boltzmann constant is represented as k_B which is approximately equal to 1.381x10²³J/K, relates the average kinetic energy of particles in a gas with the temperature of the gas. It is crucial in statistical mechanics and thermodynamics.

Syntax

Following is the syntax of calculating the Boltzmann Constant with the help of Scipy −

scipy.constants.Boltzmann

Example

In this example we are calculating the Boltzmann constant with the help of scipy method scipy.constants.Boltzmann −

from scipy.constants import Boltzmann

# Print the Boltzmann constant
print(f"The Boltzmann constant (k) is: {Boltzmann}")

Following is the output of the above program −

The Boltzmann constant (k) is: 1.380649e-23

Gas Constant

Gas Constant is denoted as R,is a fundamental constant that appears in the ideal gas law equation. It relates the pressure, volume and temperature of an ideal gas to the number of moles.

The gas constant provides a bridge between macroscopic and microscopic descriptions of gases. The value of Gas constant is given as 8.314462618 (J/(molK)).

Syntax

Here is the syntax of calculating the Gas Constant with the help of Scipy −

scipy.constants.gas_constant

Example

Below is the example of calculating the Gas constant by using the scipy.constants.gas_constant method availabe in scipy −

from scipy.constants import gas_constant

# Print the Gas Constant
print(f"The Gas Constant (R) is: {gas_constant}")

Following is the output of the above program −

The Gas Constant (R) is: 8.314462618

Elementary Charge(e)

Elementary Charge denoted as , which is the magnitude of the electric charge of a proton or the negative charge of an electron.

It is a fundamental constant in electromagnetism and quantum mechanics. The value of Elementary Charge is given as 1.602176634e-19 (Coulombs).

Syntax

Here is the syntax of calculating the Elementary Charge with the help of SciPy −

scipy.constants.e

Example

Here is the example of calculating the Elementary Charge using the method scipy.constants.e−

from scipy.constants import e

# Print the elementary charge
print(f"The elementary charge (e) is: {e}")

Following is the output of the above program −

The elementary charge (e) is: 1.602176634e-19

List of Mathematical Constants

There are many more Mathematical constants but here in this tutorial we discussed about few Mathematical constants which can be used with the help of SciPy library.

We can get all the constants available in the scipy.constants module which include Mathematical Constants, with the help of below code −

import scipy
from scipy import constants
print(dir(scipy.constants))

Following are the constants list −

['Avogadro', 'Boltzmann', 'Btu', 'Btu_IT', 'Btu_th', 'ConstantWarning', 'G', 'Julian_year', 'N_A', 'Planck', 'R', 'Rydberg', 'Stefan_Boltzmann', 'Wien', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', '_codata', '_constants', '_obsolete_constants', 'acre', 'alpha', 'angstrom', 'arcmin', 'arcminute', 'arcsec', 'arcsecond', 'astronomical_unit',.....................................
........................................................
 'u', 'unit', 'value', 'week', 'yard', 'year', 'yobi', 'yocto', 'yotta', 'zebi', 'zepto', 'zero_Celsius', 'zetta']