SciPy - Morphological Filters

---

---

Morphological Filters

Morphological filters in image processing are a set of operations that process images based on their shapes and structures. These operations are particularly useful in the context of binary or grayscale images where the primary focus is on the shapes and structures of objects in the image such as boundaries, holes and small objects.

SciPy provides morphological operations through the scipy.ndimage module which includes several functions to perform basic morphological operations. These operations are typically applied to binary or grayscale images.

Common Morphological Operations

Morphological operations manipulate an image based on its shapes and structures which is typically for binary images or grayscale images. These operations rely on a structuring element i.e., a small kernel that defines the operation's effect on the image. Here are the most common morphological operations −

• Dilation: This operation expands the boundaries of bright regions (foreground objects).
• Erosion: It shrinks the boundaries of bright regions.
• Opening: This is the erosion followed by dilation which removes small objects i.e., noise.
• Closing: This is dilation followed by erosion which fills small holes.
• Morphological Gradient: This performs the difference between dilation and erosion by highlighting the edges.

Structuring Element

In Morphological Filtering a structuring element or kernel which is a small matrix or array that defines the neighborhood over which a morphological operation is applied. The choice of the structuring element significantly affects the results of morphological operations such as dilation, erosion, opening and closing.

In scipy.ndimage structuring elements can be customized and are often defined using functions such as generate_binary_structure() or manually created as NumPy arrays.

Syntax

Following is the syntax for the function generate_binary_structure() to create a structuring element −

scipy.ndimage.generate_binary_structure(rank, connectivity)

Here are the parameters of the function scipy.ndimage.generate_binary_structure() −

• rank(int): The dimensionality of the structuring element such as 2 for 2D, 3 for 3D, etc.
• connectivity(int): This parameter determines the type of connectivity or neighborhood. 1 includes only the nearest neighbors in each dimension i.e., cross-shaped neighborhood in 2D and 2 includes diagonal neighbors i.e., full square or cube neighborhood in 2D or 3D.

Return Value

This function returns a NumPy array of shape (3,) * rank containing True and False by representing the structuring element.

2D Structuring Element with Connectivity 1

A 2D structuring element with connectivity 1 is a small matrix that defines a cross-shaped neighborhood. It includes the center pixel and the immediate horizontal and vertical neighbors but excludes the diagonal neighbors.

Here is the example which shows how we can create such a structuring element using scipy.ndimage.generate_binary_structure() with rank=2 (for 2D) and connectivity=1 −

from scipy.ndimage import generate_binary_structure

# Create a 2D structuring element with connectivity=1
structure_2d = generate_binary_structure(rank=2, connectivity=1)
print("2D Structuring Element (Connectivity=1):\n", structure_2d)

Following is the output of the 2D sturcturing element with connectivity 1 −

2D Structuring Element (Connectivity=1):
 [[False  True False]
 [ True  True  True]
 [False  True False]]

Dilation with generate_binary_structure() Function

As we discussed before the structuring element created by generate_binary_structure() is often used in binary morphological operations such as dilation, erosion, opening and closing. The choice of connectivity affects how neighboring pixels are considered during these operations.

Following is the example of the Structuring element which is used in the Dilation −

import numpy as np
from scipy.ndimage import binary_dilation
import matplotlib.pyplot as plt
from scipy.ndimage import generate_binary_structure

# Create a binary image
image = np.zeros((10, 10), dtype=int)
image[4:6, 4:6] = 1  # Small square in the center

# Generate a structuring element with connectivity=1
structure = generate_binary_structure(rank=2, connectivity=1)

# Apply dilation
dilated_image = binary_dilation(image, structure=structure)

# Plot the results
plt.figure(figsize=(10, 5))

# Original image
plt.subplot(1, 2, 1)
plt.title("Original Image")
plt.imshow(image, cmap='gray')
plt.axis('off')

# Dilated image
plt.subplot(1, 2, 2)
plt.title("Dilated Image (Connectivity=1)")
plt.imshow(dilated_image, cmap='gray')
plt.axis('off')

plt.show()

Following is the output of the 2D structuring element with connectivity 1 −

Enlarging of Structuring Element

Enlarging a structuring element in morphological operations increases the area of influence by allowing the operation to act on a broader region in the image. This is useful in tasks like filling larger gaps, expanding shapes or removing noise from larger regions.

In SciPy the function scipy.ndimage.iterate_structure() is used to enlarge structuring elements. It dilates the original structuring element by a specified number of iterations effectively by increasing its size.

Syntax

Following is the syntax of the function scipy.ndimage.iterate_structure() which is used to enlarge the structuring element −

scipy.ndimage.iterate_structure(structure, iterations)

Following are the parameters of the function scipy.ndimage.iterate_structure() −

• structure(ndarray): The input structuring element which is a binary (boolean) array. It defines the shape that will be used for morphological operations.
• iterations(int): The number of times the structuring element should be dilated and increasing the number of iterations then it will enlarge the structuring element.

This function returns the dilated structuring element after iterations dilations.

Example

Following is the example which shows how to use the scipy.ndimage.iterate_structure() function to the enlarge the structuring element generated using the scipy.ndimage.generate_binary_structure() function −

from scipy.ndimage import generate_binary_structure, iterate_structure
import matplotlib.pyplot as plt

# Step 1: Create a 2D cross-shaped structuring element
struct_2d = generate_binary_structure(rank=2, connectivity=1)
print("Original Structuring Element:\n", struct_2d)

# Step 2: Enlarge the structuring element by 2 iterations
enlarged_struct = iterate_structure(struct_2d, iterations=2)
print("Enlarged Structuring Element (2 iterations):\n", enlarged_struct)

# Step 3: Visualize the structuring elements
plt.figure(figsize=(10, 5))

# Original structuring element
plt.subplot(1, 2, 1)
plt.title("Original Structuring Element")
plt.imshow(struct_2d, cmap='gray')
plt.axis('off')

# Enlarged structuring element
plt.subplot(1, 2, 2)
plt.title("Enlarged Structuring Element")
plt.imshow(enlarged_struct, cmap='gray')
plt.axis('off')

plt.show()

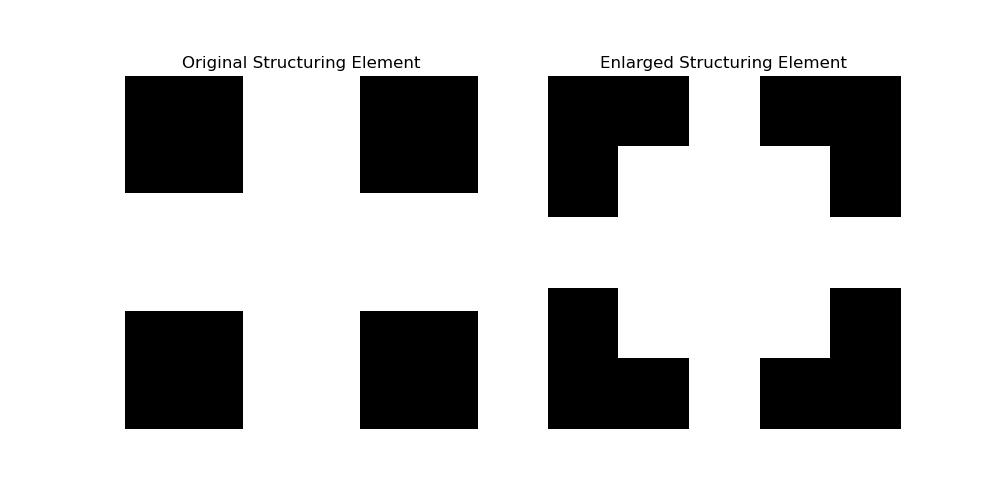
Following is the output of the enlarged structuring element with the help of scipy.ndimage.iterate_structure() function −

 Original Structuring Element:
 [[False  True False]
 [ True  True  True]
 [False  True False]]
Enlarged Structuring Element (2 iterations):
 [[False False  True False False]
 [False  True  True  True False]
 [ True  True  True  True  True]
 [False  True  True  True False]
 [False False  True False False]]

Applications of Morphological Filters

Morphological filters are widely used in image processing for analyzing and modifying the geometric structure of objects in an image. They are particularly effective in tasks involving shape, structure and segmentation. Here are the few applications of the Morphological Filters −

• Noise Removal: By using opening and closing operations, small noise elements can be removed or small holes can be filled.
• Edge Detection: The morphological gradient can be used to highlight edges in the image.
• Shape Analysis: These operations are often used in object recognition, segmentation and feature extraction.
• Pre-processing: In many computer vision tasks the morphological operations helps to prepare the image for further analysis.

Implementing Morphological Filters in SciPy

Morphological filters are powerful tools in image processing which are used for shape analysis, noise removal and enhancing image structures. In SciPy library, these operations can be performed using the scipy.ndimage module.

Following are the functions available in scipy.ndimage module to perform the Morphological Operations in image processing −

S.No.	Function & Description
1	scipy.ndimage.binary_erosion() Perform erosion on a binary image (shrinking).
2	scipy.ndimage.binary_dilation() Perform dilation on a binary image (expanding).
3	scipy.ndimage.binary_opening() Perform binary opening i.e., erosion followed by dilation.
4	scipy.ndimage.binary_closing() Perform binary closing i.e., dilation followed by erosion.
5	scipy.ndimage.grey_erosion() Shrinks bright regions in the image.
6	scipy.ndimage.grey_dilation() Expands bright regions in the image.
7	scipy.ndimage.grey_opening() Perform grayscale opening, removing small bright spots.
8	scipy.ndimage.grey_closing() Perform grayscale closing, filling small dark holes.
9	scipy.ndimage.label() Label connected components in a binary image or multi-dimensional array.
10	scipy.ndimage.find_objects() Return slice objects corresponding to the labeled regions in an array.