SciPy Physical Constants

---

---

The scipy.constants module provides access to fundamental physical constants and it also ensures that these values are maintained with the highest accuracy and are regularly updated according to the latest scientific standards.

The constants such as Planck constant, Speed of light etc, play a critical role in converting between units, performing precise calculations and modeling physical phenomena.

Using these standardized constants, scientists and engineers can ensure that their results are consistent with those obtained globally, facilitating collaboration and reproducibility in research.

This module also includes conversion factors allowing seamless transitions between different units of measurement by further enhancing its utility in scientific computation. Following are the different Physical Constants and let's see them in detail −

Planck Constant (h)

Planck Constant is denoted as h,which is a fundamental constant in quantum mechanics. This constant value is 6.626 x 10^-34Js that relates the energy of a photon to its frequency. It is essential in the study of quantum phenomena.

Syntax

Here is the syntax of calculating the Planck Constant with the help of Scipy −

scipy.constants.Planck

Example

Below is the example of calculating the Planck constant by using the scipy.constants.Planck method available in SciPy −

from scipy.constants import Planck

# Print the Planck constant
print(f"The Planck constant (h) is: {Planck}")

Following is the output of the above program −

The Planck constant (h) is: 6.62607015e-34

Planck Mass

Planck massis a natural unit of mass in the system of Planck units which is used in theoretical physics. It is the mass at which the gravitational force between two objects is comparable to other fundamental forces such as electromagnetism.

Theoretically the value of Planck Massis given as 2.176434x10^-8 Kilograms. Following is the formula for calculating the Planck Mass(mp) −

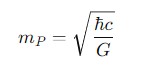
Where −

• (h-bar): is the reduced Planck constant.
• c: is the speed of light in a vacuum.
• G: is the gravitational constant.

Example

We know that there is no direct method to calculate the Planck mass with the help SciPy but we can calculate it by using the fundamental constants hbar, c and G. Below is the example −

from scipy.constants import hbar, c, G

# Calculate Planck mass
m_planck = (hbar * c / G)**0.5

print(f"Planck mass: {m_planck} kg")

Following is the output of the above program −

Planck mass: 2.1764343427178984e-08 kg

Speed of Light

Speed of Light in a vacuum is a fundamental constant that represents the maximum speed at which all energy, matter and information in the universe can travel. It is a critical value in both classical and modern physics particularly in the theory of relativity.

The speed of light in a vacuum is approximately given as 299,792,458 meters per second. Following is the mathematical formula for calculating the speed of light −

E = pc

Where −

• E: is the energy of the photon.
• p: is the momentum of the photon
• c: is the speed of light.

Syntax

Following is the syntax of calculating the speed of light with the help of Scipy −

scipy.constants.c

Example

Below is the example of calculating the speed of light with the help of scipy.constants.c method −

from scipy.constants import c
print(f"Speed of light (c): {c} meters per second")

Following is the output of the above program −

Speed of light (c): 299792458.0 meters per second

Gravitational Constant (G)

The Gravitational constant is a fundamental constant used in Newton's law of universal gravitation. It is denoted as G. It describes the strength of the gravitational force between two masses.

The gravitational constant is approximately given as 6.67430x10^-11m³kg^-1s^-2. The mathematical formula for finding the Gravitational Constant is given as follows −

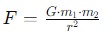
Where −

• F: It is the gravitational force between two masses m1 and m2.
• r: It is the distance between the centers of the two masses.
• G: It is the gravitational constant.

Syntax

Following is the syntax of Gravitational Constant in Scipy −

scipy.constants.G

Example

Below is the example which shows how to find the gravitational constant with the help of scipy.constants.G method −

from scipy.constants import G
print(f"Gravitational constant (G): {G} m^3 kg^-1 s^-2")

Following is the output of the above program −

Gravitational constant (G): 6.6743e-11 m^3 kg^-1 s^-2

Permeability of Free Space ()

The Permeability of free space is also known as the magnetic constant which is a physical constant that describes the ability of a vacuum to support the formation of a magnetic field.

It is denoted by the symbol (). It is a fundamental parameter in electromagnetism. The value of permeability of free space is approximately given by 4 x 10^-7. The mathematical formula for finding the Permeability is given as follows −

B=0H

Where −

• B: is the magnetic flux density (or magnetic field)
• H: is the magnetic field strength.

Syntax

Following is the syntax of Permeability of Free Space in Scipy −

scipy.constants.mu_0

Example

Below is the example which shows how to find the Permeability using the method scipy.constants.mu_0 which is availabe in Scipy −

from scipy.constants import mu_0
print(f"Permeability of free space (): {mu_0} H/m")

Following is the output of the above program −

Permeability of free space (): 1.25663706212e-06 H/m

Permittivity of Free Space ()

The Permittivity of free space is also known as the electric constant which is a fundamental physical constant that describes how electric fields interact with the vacuum. It is denoted by the symbol . It is a measure of the ability of a vacuum to permit electric field lines.

The value of Permittivity of free space is approximately given as 8.85418781710^-12F/m. In Scipy it is represented as epsilon_0.Following is the formula for calculating the Permittivity mathematically −

B=0H

Where −

• B: It is the magnetic flux density (or magnetic field)
• H: It is the magnetic field strength.

Syntax

Following is the syntax of Permittivity of Free Space in Scipy −

scipy.constants.mu_0

Example

Here is the example of calculating the Permittivity of free space by using the scipy.constants.epsilon_0 method −

from scipy.constants import epsilon_0
print(f"Permittivity of free space (): {epsilon_0} F/m")

Following is the output of the above program −

Permittivity of free space (): 8.8541878128e-12 F/m

Fine-Structure Constant ()

The Fine-Structure Constant is a dimensionless fundamental physical constant characterizing the strength of the electromagnetic interaction between elementary charged particles. It is a key parameter in quantum electrodynamics (QED) and reflects the coupling strength of the electromagnetic force. It is denoted by the symbol .

The value of Fine-Structure Constant () is approximately given as 0.0072973525693. In Scipy it is represented as alpha.Following is the formula for calculating the Fine-Structure Constant mathematically −

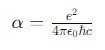
Where −

• e: It is the elementary charge.
• : It is the permittivity of free space.
• (h-bar): It is the reduced Planck's constant.
• c: It is the speed of light in a vacuum.

Syntax

Following is the syntax of Fine-Structure Constant () in Scipy −

scipy.constants.alpha

Example

Below is the example of calculating the Fine-Structure Constant () by using the scipy.constants.alpha method −

from scipy.constants import alpha
print(f"Fine-Structure Constant (): {alpha}")

Following is the output of the above program −

Fine-Structure Constant (): 0.0072973525693

List Of Physical Constants

Here in this tutorial we discussed about only few physical constants which can be used with the help of SciPy library. There are many other such as Stefan-Boltzmann Constant (), Reduced Planck's Constant (), Magnetic Constant (_0), Electric Constant (_0) and so on.

We can get all the constants available in the scipy.constants module with the help of below code −

import scipy
from scipy import constants
print(dir(scipy.constants))

Following are the constants list −

['Avogadro', 'Boltzmann', 'Btu', 'Btu_IT', 'Btu_th', 'ConstantWarning', 'G', 'Julian_year', 'N_A', 'Planck', 'R', 'Rydberg', 'Stefan_Boltzmann', 'Wien', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', '_codata', '_constants', '_obsolete_constants', 'acre', 'alpha', 'angstrom', 'arcmin', 'arcminute', 'arcsec', 'arcsecond', 'astronomical_unit',.....................................
........................................................
 'u', 'unit', 'value', 'week', 'yard', 'year', 'yobi', 'yocto', 'yotta', 'zebi', 'zepto', 'zero_Celsius', 'zetta']