Scipy - Single Integration (quad)

---

---

Single Integration in SciPy

SciPy's Single Integration can be done with the help of quad() function which is a powerful tool used for one-dimensional numerical integration i.e. definite integrals. It is part of the scipy.integrate module and is based on adaptive quadrature methods.

This function computes the integral of a given function over a specified range by returning both the integral's result and an estimate of the error. It is especially useful for smooth functions over finite limits and handles both simple and complex integrands.

The quad() function is widely used in scientific computing for tasks involving the integration of continuous functions. Mathematically the quad() function evaluates definite integrals of the form as follows −

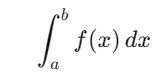
Syntax

Following is the syntax of the scipy.integrate.quad() function which is used to calculate the Single Integration −

scipy.integrate.quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50, complex_func=False)

Parameters

Here are the parameters of the scipy.integrate.quad() function −

• func: The function to integrate. It should accept a single argument and return a scalar.
• a: The lower limit of integration (float).
• b: The upper limit of integration (float).
• args(Optional): A tuple of additional arguments to pass to the function.
• full_output(Optional): If the value is set to 1 then the output includes error estimates and additional information.
• epsabs(Optional): Absolute error tolerance. Default value is 1.49e-08.
• epsrel(Optional): Relative error tolerance. Default value is 1.49e-08.
• limit(Optional): The maximum number of subdivisions. Default value is 50.
• points(Optional): A list of points at which to evaluate the integrand.
• weight(Optional): A string specifying the type of weight function ('cauchy', 'cosine', 'chebyshev', etc.).
• wvar(Optional): A variable for the weight function.
• wopts(Optional): Options for the weight function.
• maxp1(Optional): Maximum number of poles for the weight function. Default value is 50.
• limlst(Optional): Maximum number of limit points. Default value is 50.
• complex_func(Optional): If the value is set to True then it indicates that the function is complex.

Example of Single Integration

Following is the example of finding the Single Integration of the function f(x) = sin(x) over the interval [o,] then the result will be 2 −

import numpy as np
from scipy import integrate

# Define the function to be integrated
def f(x):
    return np.sin(x)

# Perform the integration from 0 to p
result, error = integrate.quad(f, 0, np.pi)

# Display the results
print(f"Integral Result: {result}")

Below is the output of the Single Integration of the given function −

Integral Result: 2.0

Handling Infinite Limits

In scipy.integrate.quad() function, we can handle infinite limits for improper integrals by passing np.inf or -np.inf as the limits of integration.

Example

Here in this example the function e^-x is integrated from 0 to infinity which converges to 1. The quad() function is capable of handling such improper integrals will automatically applying appropriate techniques to compute them.

from scipy import integrate
import numpy as np

# Define the function to integrate
def f(x):
    return np.exp(-x)

# Perform the integration with an infinite upper limit
result, error = integrate.quad(f, 0, np.inf)

print("Integral Result:", result)  # Output: 1.0
print("Estimated Error:", error)   # Output: Estimated error in the result

Here is the output of handling the infinite limits in single Integration in scipy −

Integral Result: 1.0000000000000002
Estimated Error: 5.842606701570796e-11

Error Tolerances

In scipy.integrate.quad() the error tolerances are controlled by two optional parameters namely, epsabs and epsrel. These parameters define the absolute and relative error tolerance by ensuring the result's precision.

• epsabs: Absolute error tolerance. The algorithm stops when the absolute error estimate is below this value. Default value is 1.49e-08.
• epsrel: Relative error tolerance. The algorithm stops when the relative error estimate is below this value. Default value is 1.49e-08.

The integration stops when the absolute error is less than epsabs or when the relative error is less than epsrel. We can adjust these values to increase precision or speed up computation.

Example

In this example we set both epsabs and epsrel to 1e-6 which means the integration will continue until the error estimate is smaller than these tolerances −

from scipy import integrate
import numpy as np

# Define the function to integrate
def f(x):
    return np.exp(-x)

# Perform the integration with an infinite upper limit
result, error = integrate.quad(f, 0, np.inf)

print("Integral Result:", result)  # Output: 1.0
print("Estimated Error:", error)   # Output: Estimated error in the result

Below is the output of the Error Tolerance of single integration −

Integral Result: 2.0
Estimated Error: 2.220446049250313e-14

Complex Functions

In scipy.integrate.quad() we can integrate complex-valued functions by setting the complex_func parameter to True. This allows quad() function to handle functions that return complex numbers. The integration is performed separately for the real and imaginary parts of the function.

Example

In this example we will integrate e^ix from 0 to by demonstrating how to handle complex-valued integrals using SciPy's quad() function.

from scipy import integrate
import numpy as np

# Define a complex function
def complex_function(x):
    return np.exp(1j * x)  # e^(ix)

# Perform the integration from 0 to p with complex function handling
result, error = integrate.quad(complex_function, 0, np.pi, limit=100, complex_func=True)

print("Integral Result:", result)
print("Estimated Error:", error)

Here is the output of the Complex functions single integration in scipy −

Integral Result: (3.6775933888827275e-17+2j)
Estimated Error: (2.2102239425853306e-14+2.220446049250313e-14j)

Finally we can conclude the SciPys quad() function is highly versatile, capable of efficiently handling smooth functions, improper integrals, complex-valued functions and even providing detailed diagnostics. Its ideal for situations where analytic solutions to integrals are difficult or impossible to obtain by making it a fundamental tool in numerical computation.